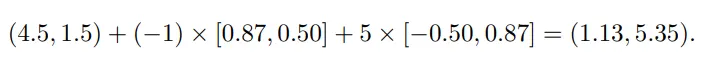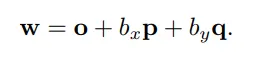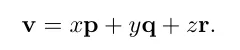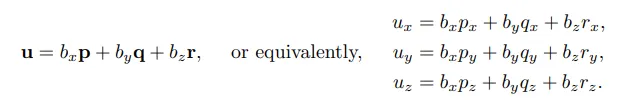앞에서 우리는 좌표 공간에 이야기를 나누었습니다.
이 장에서 우리는 게임과 그래픽스에서 자주 사용되는 여러 좌표공간에 대해서 소개 하겠습니다.
우리는 한 좌표 공간에서 다른 좌표공간으로 이동하는 과정을 이야기 할 것입니다.
1.
좌표계 변환에 대한 정의를 설명합니다.
2.
게임에서 사용되는 좌표계 4가지에 대해서 설명합니다. (world space, object space, camera space, upright space)
3.
좌표계 공간 변환에대해 설명합니다.
Object Space(Local Space) 오브젝트 공간
오브젝트 공간은 특정 오브젝트만을 그리기위한 정정정보가 포함된 공간입니다.
정확히는 하나의 공간에 오브젝트(물체, 캐릭터등등) 하나의 오브젝트만을 원점에 두어서 물체를 그린 공간입니다. 사람을 기준으로 사람 한명이 중심이라고 생각하고 각각의 사람이 하나의 오브젝트 공간의 주인공이 되는 겁니다.
만약에 우리가 한 사람에게 “한 걸음 앞으로 이동 해보세요” 라고 말하면 그 사람은 자신의 오브젝트 공간에서 어떤 방향으로 움직일지 알수 없습니다. (앞이라는건 개개인에 따라서 상대적이기 떄문입니다) 누군가는 북쪽으로 이동하고, 누군가는 서쪽으로 이동하고 각각 방향이 다를 것 입니다.
누군가 왼쪽으로 가라고 말하는건 오브젝트 공간에서의 움직임을 이야기하고
누군가 서쪽으로 가라고 말하는건 월드 공간에서의 움직임을 이야기 합니다.
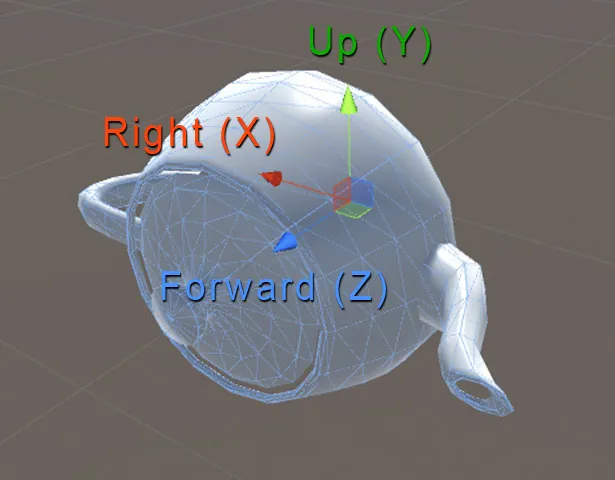
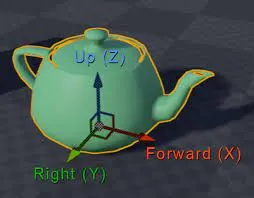
보통 오브젝트 공간에서는 오브젝트 공간 내에서 기준이 방향을 정하기 위해서 임의로 방향을 정해줍니다. Foward(앞), Right(오른쪽), Up(위) 가 됩니다. 보통은 만드는 사람에 의해서 정해지지만 캐릭터, 자동차 같은 통상적으로 정해져 있습니다.
World Space(월드 공간)
저는 지금 이 글을 서울 특별시 구로구 오류동에서 작성을 하고 있습니다. 이러한 주소는 우리나라 안에서 절대적인 위치를 표현하고 있습니다.
지구상에서 원점(0,0)은 영국의 그리니치 마을의 왕립 천문대의 위치를 기준으로 잡고 있습니다.
이러한 월드(세상)을 기준으로 계산하는 좌표시스템은 매우 특별합니다. 어디에서든지 공통적으로 사용이 되는 약속이된 자표계 입니다. 즉 우리는 약속된 좌표계가 있다면 각자의 어떤 좌표계에서든지 해당 좌표계로 옮긴다면 절대적인 위치를 지정할 수 있습니다.
우리는 앞서서 절대적인것 없다고 이야기 했습니다. 하지만 여기서 world는 모든 물체들이 모이는 하나의 세계(공간)으로 정의하고 진행하겠습니다.
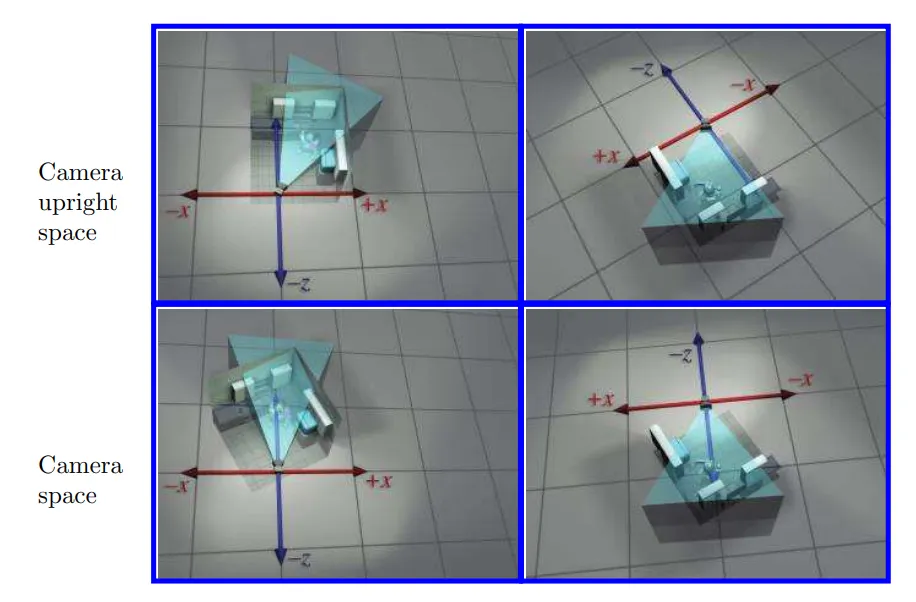
Camera Space(카메라 공간)
오브젝트 공간의 중요한 점은 오브젝트가 0,0,0 의 원점 위치에 있다는 것이 사실은 오브젝트 공간이 아닌 카메라공간이라는 것입니다. 즉 바라보는 사람도 0,0,0에 위치하고 오브젝트도 0,0,0에 있다면 물체는 같은 위치에 있기에 보이지 않아야 합니다.
그래서 사실은 우리가 0, 0, 0을 바라보고 있다는건 물체를 바라보기 위한 눈이 있다는 점이죠.
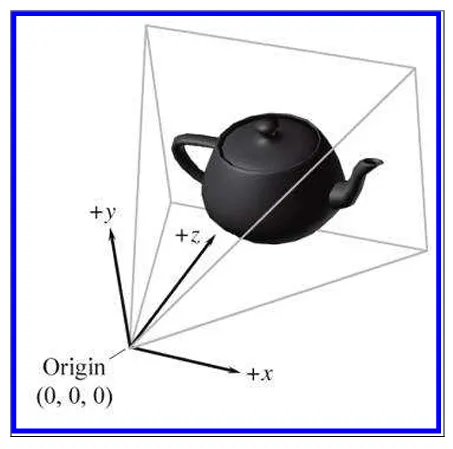
일반적인 왼손 좌표계에서는 앞방향을 +z, 로 둡니다. 위를 +y, 오른쪽을 +z
여기서 카메라 공간을 변환함에 있어 3D 카메라공간(projection) 또는 2D(orthgonal) 카메라공간으로 변환할때 프로젝션 이라는 변환을 거쳐야 합니다. 이는 나중에 뒷부분에서 더 자세하게 설명할 예정입니다.
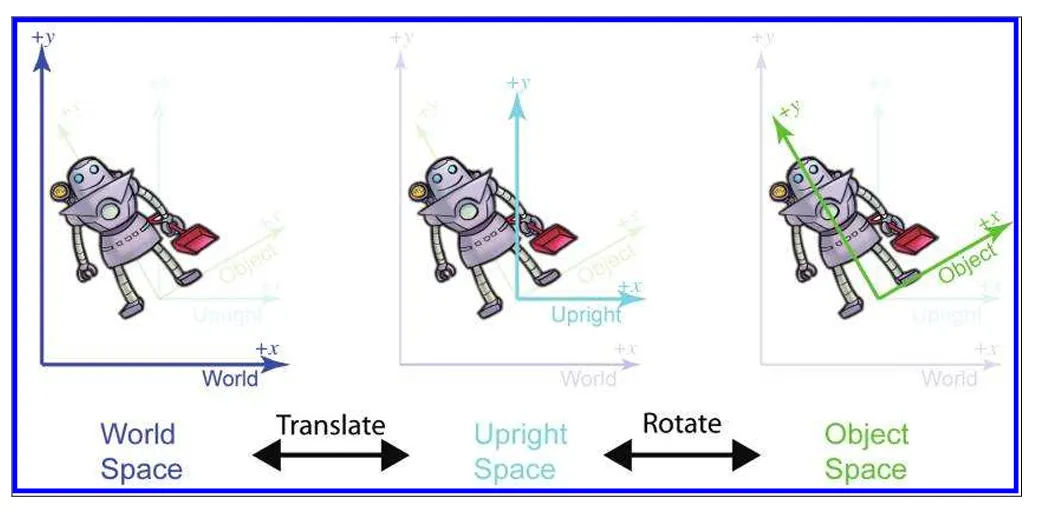
Upright Space(업라이트 공간)
때로는 용어가 명확하지 않아서 해결하지 못하는 문제가 많습니다. Don Knuth는 자주 사용 되는 개념에 이름을 부여하는 “명명하고 해결하라” 라는 문구를 만들 었습니다.
3D 그래픽스에서 "upright space"는 일반적으로 월드 좌표계(world coordinate system) 와 오브젝트 공간(Object space) 사이에 존재합니다. 또는 월드 공간(world space)에서의 "수직 방향"과 같은 축을 가지고 있습니다.
오브젝트 공간에서 업라이트 공간으로 변환하는데 있어서는 물체의 회전정보만 필요로 합니다.
그리고 업라이트 공간에서 월드 공간으로 변환하는데 있어서는 축을 재정립시키는 것 뿐입니다.
월드 좌표계와 Upright Space
•
월드 좌표계에서는 X, Y, Z 세 축을 사용해 공간을 정의합니다.
•
대부분의 3D 엔진과 툴에서는 Y축이 수직(위쪽 방향)을 나타내는 것이 일반적입니다. 이 경우, "upright space"는 Y축을 따라 정렬된 공간 또는 오브젝트를 의미할 수 있습니다.
예를 들어:
•
캐릭터나 오브젝트가 Y축을 기준으로 서 있다면, 이는 "upright"하게 배치된 것으로 간주됩니다.
•
3D 모델링 프로그램이나 게임 엔진에서 "upright space"를 고려해 오브젝트를 배치하거나 회전할 때, 오브젝트가 Y축을 따라 올바르게 정렬되어 있는지 확인하는 것이 중요합니다.
그러나 일부 시스템에서는 Z축이 수직 방향을 나타내기도 하므로, "upright space"의 정의는 사용되는 좌표계의 관습에 따라 달라질 수 있습니다.
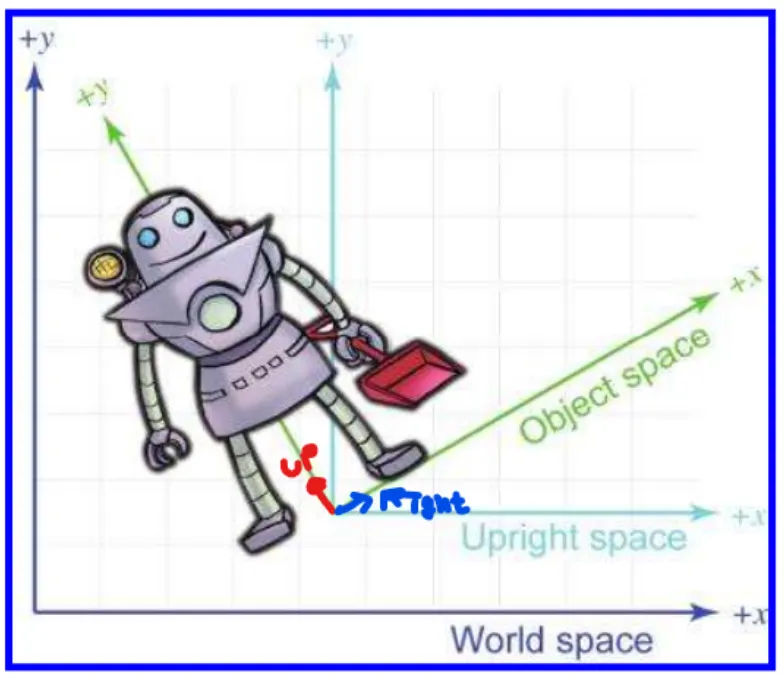
Basis Vectors and Coordinate Space Transformations(기저벡터와 좌표공간 변환)
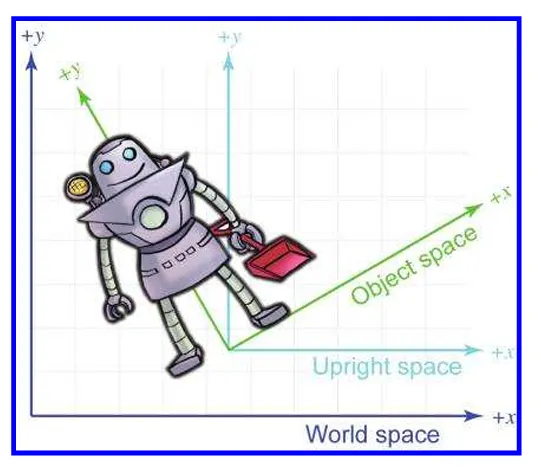
로봇이 샌드위치를 잡는 동작을 렌더링한다고 생각해 봅시다. 조명에 의해서 명암을 계산할 때 우리는 로봇의 오브제그 공간 내에서가 아니라 로봇을 월드에 배치시켜서 조명계산을 해야합니다. 그렇다면 월드에서의 빛의 위치를 알아야 합니다.
이것은 동전의 양면의 문제와 같습니다. 우리는 오브젝트 공간에서 → 월드 공간으로의 좌표변환이 가능해야 합니다.
위 내용을 사진과 함께 알아 봅시다.
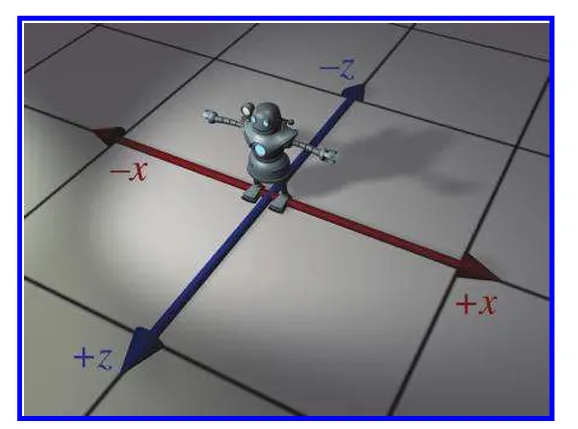
다음 그림과 같이 아티스트는 로봇을 월드공간에서 원점에 두고 작업을 합니다.
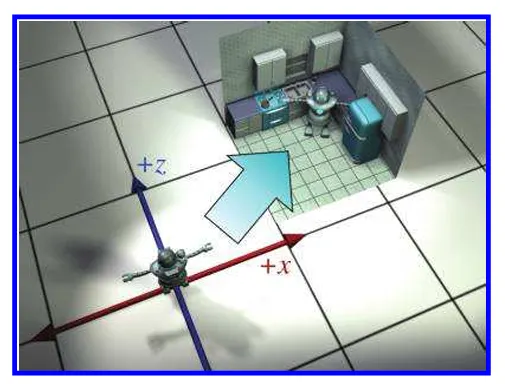
그리고 로봇을 집안의 위치로 배치하여 여러개의 오브젝트들이 한곳에 모이도록 만듭니다.
부록 : (왼손좌표계 사용) [x, y, z]
그럼 해당 과정을 여러 순서로 나누어서 보도록 하겠습니다.
우리의 목표는 로봇의 정점들을 새로운 위치로 변환하는 것입니다. (부엌으로 옮긴다)
이에 있어서 수학적으로 깊이 들어가 설명을 하진 않겠습니다. 그부분은 다음 단원인 행렬에서 설명하도록 하겠습니다.
로봇을 부엌으로 위결과와 같이 이동시키려면 일단 제자리에서 120도를 회전시켜야합니다.
그리고 우리는 우측 위쪽 방향으로 로봇을 이동시킵니다. 해당 값은 [18, 0, 10] 값이 됩니다.
여기서 주의 깊게 봐야 할것은 “먼저 회전을 한다음에 이동해야 하나요?” 입니다.
통상적으로 우리는 이동이 더 친근한 연산이기 떄문에 회전하기 전에 이동하는게 자연스러워 보일수 있지만 회전을 먼저 진행해주는것이 더 계산과 이해가 쉽습니다.
그 이유는 다음과 같습니다. 먼저 물체를 회전 할때 회전 중심은 원점이 됩니다.
이동을 먼저 진행 한후에 회전하면 해당 회전은 원점이 아닌 점을 중심으로 회전하게 됩니다. 그러면 복잡한 계산과정을 거치게 됩니다.
그 이유는 원점에서의 회전은 원점의 대한 선형변환입니다. 하지만 원점이 축이 아닌 회전은 아핀변환이기도 하다는 것입니다.
선형변환과 아핀변환
1. Linear Transform (선형 변환)
•
정의: 선형 변환은 원점을 그대로 유지하면서 벡터를 다른 벡터로 변환하는 과정입니다. 주어진 벡터에 대해 회전, 스케일링(확대/축소), 반사 등을 수행할 수 있습니다.
•
수학적 표현: 선형 변환은 행렬 A로 표현되며, 벡터 x에 대해 다음과 같이 표현됩니다:
•
특징:
◦
원점이 그대로 유지됩니다.
◦
직선은 직선으로, 평면은 평면으로 변환됩니다.
◦
선형 변환에는 이동(Translation)이 포함되지 않습니다.
2. Affine Transform (아핀 변환)
•
정의: 아핀 변환은 선형 변환에 이동(Translation)을 추가한 변환입니다. 좌표를 이동시킬 수 있어 더 일반적인 변환입니다.
•
수학적 표현: 아핀 변환은 선형 변환 행렬 A와 이동 벡터 b를 사용하여 다음과 같이 표현됩니다:
•
특징:
◦
이동(Translation)을 포함하기 때문에 원점이 다른 위치로 이동할 수 있습니다.
◦
직선은 직선으로, 평면은 평면으로 변환되지만, 위치가 바뀔 수 있습니다.
◦
아핀 변환은 선형 변환의 모든 특성을 포함하면서 더 일반적입니다.
주요 차이점 요약:
•
원점: 선형 변환은 원점을 이동시키지 않지만, 아핀 변환은 원점을 다른 위치로 이동시킬 수 있습니다.
•
수학적 표현: 선형 변환은 단순히 행렬 곱셈으로 표현되지만, 아핀 변환은 행렬 곱셈에 벡터 덧셈이 추가됩니다.
•
적용 범위: 선형 변환은 회전, 스케일링, 반사 등만 가능하지만, 아핀 변환은 이 모든 것에 이동(Translation)까지 포함합니다.
그럼 원점이 아닌 상태에서 회전을 올바르게 진행하려면 어떻게 해야 할까요?
방법은 임의의 위치에 점에 대한 회전의 경우 회전의 중심을 원점으로 두고 회전 시킨후에 다시 해당위치로 변환합니다.
1.
이동
2.
회전 (원점이 아닌 점을 중심으로 회전하기 떄문에 중심을 원점으로 변환해야 한다.)
2.1 로봇을 원점으로 이동시킨다.
2.2 원점에서 회전시킨다.
2.3 다시 기존위치로 이동시킨다.
이렇게 2가지 방법으로 해서 우리는 로봇을 부엌에 올바른 위치에 옮길수 있게 되었습니다.
하지만 이는 월드 공간에서의 원점을 중심으로 물체가 배치된 상태입니다. 우리가 보는 눈(카메라)에서의 원점으로의 선형변환을 진행해야 합니다.
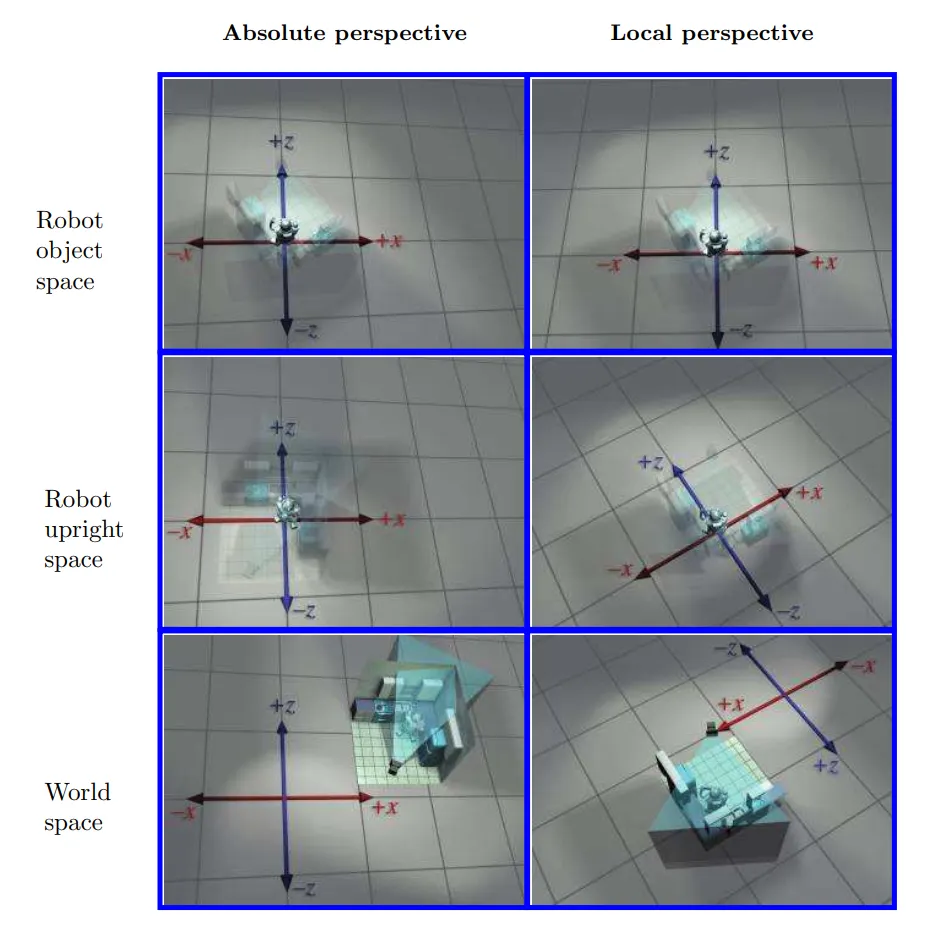
왼쪽은 외부 관점에서 본것이고 오른쪽은 카메라가 바라보는 관점에서 보는것 입니다.
모델을 월드에 배치하는건 쉬웠습니다. 그럼 어떻게 월드공간에서 카메라공간으로 이동시킬수 있을까요?
생각 해보면 매우 간단합니다. 오브젝트 자체는 원래 원점에 있던걸 좌표를 바꾸어 새로이 배치하여 그곳을 우리는 세계공간이라고 정의하였습니다.. 그러면 세계공간에 있는 모든 물체들을 또 다른 위치로 이동시킨후에 새로운공간(카메라공간)이라고 정의하면 됩니다.
카메라가 원점으로 이동한 거리만큼 모든 물체들도 이동시키면 카메라가 원점에 존재하게 되어 세계공간의 원점에 카메라가 존재하게 되고 곧 세계공간과 카메라공간이 같아 집니다.
이 경우에는 물체를 이동시키는 것과 다르게 회전하기전에 이동을 먼저 진행해주는것이 더 쉽습니다.
우리는 앞서 원점을 중심으로 회전시켰을 경우가 연산을 함에 있어서 더 쉽다는걸 배웠기 때문이죠.
물론 이작업의 복잡성에 대해서는 고민할 필요는 없습니다. 대부분 그래픽API를 이용해서 편하게 변환할수 있기 때문입니다.
마지막으로 카메라공간으로 변환은 끝이 아닙니다. 최종변환은 프로젝션 화면 공간이 목적지 입니다. 이는 뒷부분에서 보도록 하겠습니다.
여기서 우리는 카메라 뷰와 객체의 위치 및 방향을 처리하는 방식에서 두가지 방법이 있습니다.
Absolute Perspective와 Local Perspective가 있습니다.
1. Absolute Perspective (절대적 관점)
•
정의: 절대적 관점은 3D 공간에서 카메라나 객체의 위치와 방향을 전역 좌표계(Global Coordinate System) 기준으로 처리하는 방식입니다. 이 좌표계는 씬(Scene) 전체에 걸쳐 고정되어 있으며, 모든 객체와 카메라는 이 고정된 좌표계를 기준으로 위치와 방향을 계산합니다.
•
특징:
◦
일관된 관계: 절대적 관점에서는 모든 객체의 위치와 방향이 하나의 전역 좌표계를 기준으로 하여 계산되므로, 위치와 방향이 명확하고 일관된 관계를 가집니다.
◦
고정된 기준: 객체가 이동하거나 회전하더라도 이들은 전역 좌표계를 기준으로 측정되기 때문에, 전체적인 장면 내에서의 위치가 명확합니다.
◦
예시: 3D 씬에서 카메라가 고정된 위치에서 씬 전체를 관찰하는 경우, 또는 특정 객체가 씬의 중심을 기준으로 이동하는 경우.
2. Local Perspective (지역적 관점)
•
정의: 지역적 관점은 객체나 카메라의 위치와 방향을 그 객체의 로컬 좌표계(Local Coordinate System) 기준으로 처리하는 방식입니다. 로컬 좌표계는 객체 자체에 따라 이동하며, 객체의 이동이나 회전에 따라 좌표계도 함께 변화합니다.
•
특징:
◦
상대적 관계: 지역적 관점에서는 객체 간의 위치와 방향이 그들의 로컬 좌표계에 따라 정의되기 때문에, 객체 간의 관계를 상대적으로 이해할 수 있습니다.
◦
유연한 변환: 객체가 이동하거나 회전할 때 로컬 좌표계도 함께 이동하므로, 객체 간의 관계를 보다 유연하게 조작할 수 있습니다.
◦
예시: 캐릭터가 자신을 기준으로 주변을 탐색하거나, 로봇의 팔이 자신의 몸체를 기준으로 움직이는 경우.
3. 응용 사례
•
Absolute Perspective: 전체 씬의 배치, 월드 빌딩, 전역적 조명 계산 등 씬의 전반적인 구조를 고려해야 하는 작업에서 유용합니다.
•
Local Perspective: 개별 객체의 애니메이션, 복합적인 상호작용, 객체 내부의 세부적인 움직임을 처리할 때 사용됩니다.
4. 장단점
•
Absolute Perspective:
◦
장점: 씬의 전체적인 구조와 일관성을 유지하기 쉬우며, 복잡한 씬에서 객체의 위치를 명확하게 파악할 수 있습니다.
◦
단점: 객체 간의 관계를 처리할 때 유연성이 떨어질 수 있으며, 로컬 변환을 처리하기 복잡할 수 있습니다.
•
Local Perspective:
◦
장점: 객체 간의 상대적인 움직임을 처리하기에 적합하며, 애니메이션과 상호작용을 자연스럽게 구현할 수 있습니다.
◦
단점: 전역적인 씬 구성에서 일관성을 유지하기 어렵고, 로컬 좌표계를 이해하지 못하면 복잡해질 수 있습니다.
5. 결론
•
3D 그래픽 작업에서는 절대적 관점과 지역적 관점 모두 중요한 역할을 합니다. 전체 씬의 구성이나 전역적인 변수를 처리할 때는 절대적 관점이 유리하고, 개별 객체의 상호작용이나 애니메이션을 처리할 때는 지역적 관점이 더 효과적입니다. 작업의 성격에 따라 이 두 관점을 적절히 활용하는 것이 중요합니다.
Specifying Coordinate Spaces(좌표 공간 정의)
좌표 공간을 정의 하는 방법은 원점과 축을 지정하여 정의 합니다. 축은 벡터이며 해당 공간의 방향을 알수 있게 됩니다. 원점은 해당 공간의 중심이 되는 위치를 정의합니다.
Basis Vectors (기저 벡터)
우리는 앞서 배운 내용들로 오브젝트 좌표에서 공간좌표로 변환할 준비가 되었다.
로봇의 어꺠의 부착된 빛을 발광하는 물체의 빛계산을 위해 어꺠에 부착된 라이트의 월드좌표를 구해야한다. 로봇을 중점으로 두었을떄 오른쪽 어깨가 (-1, 5)만큼 떨어져 있다면 우리는 어떻게 해당 좌표를 구해야 하는가?
단계를 나누어서 계산해보도록 하겠다.
1.
로봇의 좌표는 (4.5, 1.5)이다.
2.
로봇 기준에서 어꺠좌표는 (-1, 5)만큼 떨어져 있다.
3.
로봇 모델 좌표계 기준에서 길이가 1인 right 방향벡터는 [0.87, 0.50], up방향벡터는 [-0.50, 0.87]이다.
4.
이를 이용 해서 로봇의 오른쪽 어꺠 좌표를 구해보면 다음과 같은 식을 통해서
(1.13, 5.35)를 구할수 있다.
자 이제 여기서 예제와 관련된 숫자들을 제거하고 문자로 치환해보도록 하겠다.
o는 물체의 좌표 위치, b는 어꺠가 위치한 좌표의 위치, p는 물체의 기준에서 오른쪽을 바라보는 길이가 1인 월드공간에서의 벡터, q는 물체의 기준에서 위쪽을 바라보는 길이가 1인 월드공간에서의 벡터 라고 정의 하겠다. 그럼 우리는 최종 월드좌표(w)를 다음과 같은 식으로 표현이 가능하다.
이를 이용해 3차원 좌표를 더욱 간단하계 표현하면 다음과 같은 식을 도출 할 수 있습니다.
p, q, r 은 3차원공간에서기준이 되는 기저벡터입니다. (위 로봇 그림에서 up, right벡터와 같은 역할을 합니다.)
공통적으로 3차원공간에서 p = [1,0,0], q = [0,1,0], and r = [0,0,1] 이 기저벡터가 됩니다.
기준이 어디인지에 따라서 p,q,r 이 다른값을 되기도 합니다.
좌표공간은 기저벡터가 바뀌면 변환됩니다. 예를 들어, 새로운 기저벡터 집합에 대해 같은 벡터의 좌표를 구하려면 기존 좌표에서 새로운 기저벡터로 변환을 해야 합니다. 이 과정은 선형변환과 관련이 있으며, 새로운 기저로 변환된 좌표는 원래 벡터와 동일한 벡터 공간 내에서 표현되지만 다른 좌표계를 사용하게 됩니다.
•
기저벡터는 벡터 공간의 차원을 정의하고, 그 공간 내 모든 벡터를 생성할 수 있는 선형 독립적인 벡터 집합입니다.
•
좌표공간은 주어진 기저벡터에 따라 벡터를 표현하는 방법이며, 벡터의 성분을 나타냅니다.
•
벡터의 좌표는 기저벡터의 선택에 따라 달라지며, 기저가 바뀌면 좌표도 변환됩니다.
두가지 예를 들어 보겠습니다.
로봇 모델의 찌그러짐 늘어나는 애니메이션을 그리고 싶다고 상상해보세요. 우리는 오브젝트 공간에 있는 정점을 변형하여 카메라공간에 배치할떄 해당 애니메이션을 활용 할 수 있습니다.
오브젝트 공간 좌표는 일정하게 유지되지만 카메라 공간 좌표는 변경되어 원하는 애니메이션을 표현하게 되겠죠.
또하나는 텍스처 매핑을 이용할떄 기저벡터를 사용합니다. 법선 매핑을 예로 들면 텍스처에서 하나의 픽셀에 저장된 법선 벡터 정보는 탄젠트 공간에 정의되어 있습니다.
이를 올바르게 해석하기 위해 탄젠트 공간 정보가 필요합니다.
렌더링 시, 법선 맵의 법선 벡터는 탄젠트 공간에서 정의되기 때문에, 이를 월드 공간이나 뷰 공간으로 변환하여 조명 계산에 사용합니다. 이 변환은 각 정점의 탄젠트, 비탄젠트, 법선 벡터를 이용하여 행렬을 구성함으로써 이루어집니다.
자세한 내용은 추후 법선매핑에서 다루겠습니다.
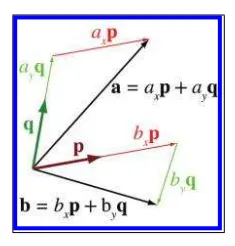
이 그림을 보면 q 와 p 벡터는 길이가 같습니다. 벡터 a와 b를 보면 xp + yq공식을 통해 이루어져 있습니다. 이는 기저벡터 p,q를 사용해 선형조합을 이루어 a,b를 만들어냅니다.
3차원 에서 표현하고 싶다면 하나의 차원을 추가함과 동시에 하나의 기저 벡터도 추가해주면 됩니다.
여기서 기저벡터 간에 수직을 이루는 벡터를 직교 기저 벡터라고 합니다.
직교 기저를 사용하면 벡터의 분해와 재구성이 쉬워지며, 계산이 간단해집니다. 특히 벡터의내적과 같이 계산이 간편해집니다. 직교 기저 벡터를 구하는 방법으로는 그램-슈미트 등이 있으며, 실제 문제해결에서 유용하게 활용됩니다.
Nested Coordinate Space(중첩 좌표 공간)
3D 공간에서 오브젝트들은 한 좌표공간에서 존재합니다. 아티스트에 의해서 모델이 만들어지고 해당 모델은 오브젝트(모델) 공간에 만들어집니다.
그러면 이 물체를 우리 게임 공간에 배치하기 위해서는 모델공간에 있는 각 점들을 월드공간으로 배치해야 합니다. 그래야 서로 물체간 상호작용이 가능해집니다.
우리가 원하는 좌표공간만을 저장해두고 계산 할 수 있지만 여러 좌표계를 동시에 계산 할수 있도록 중첩시켜서 가지고 있는게 여러가지면에서 계산하기가 편해집니다.
예를 들어 특정 오브젝 트에 대해서 빛의 세기를 계산할때는 카메라 좌표로 이동시켜서 계산을 하고
애니메이션 관련 계산을 할떄는 캐릭터 좌표(오브젝트 좌표)로 바꾸어서 계산을 하면 편리합니다.
좌표를 중첩해서 계산하는것은 이렇게 편리하게 계산할수 있게 도와줍니다.