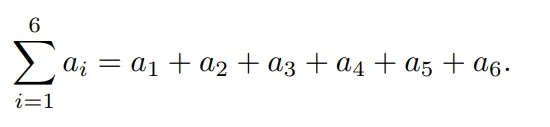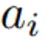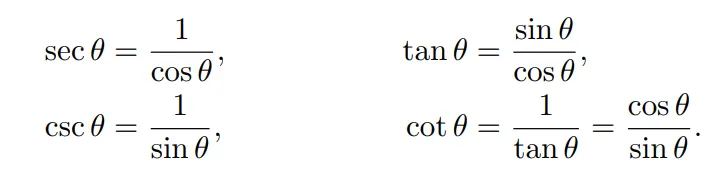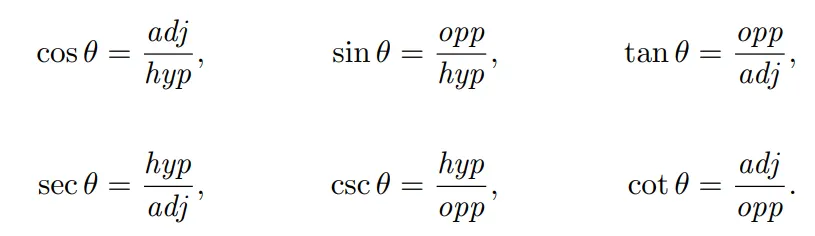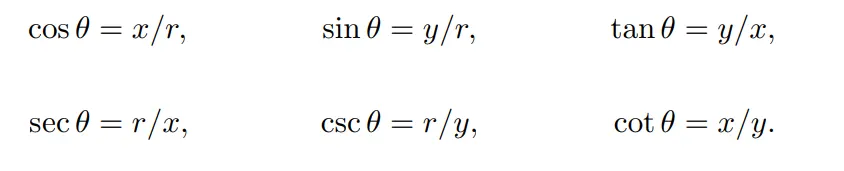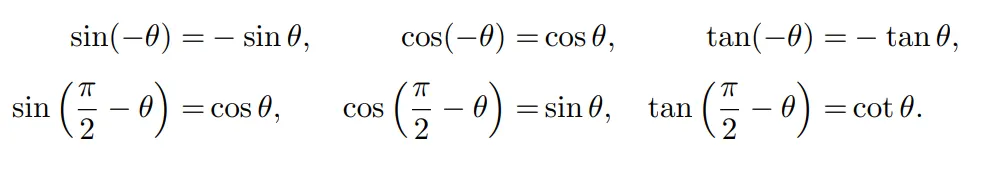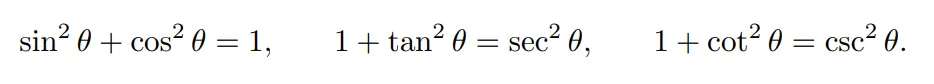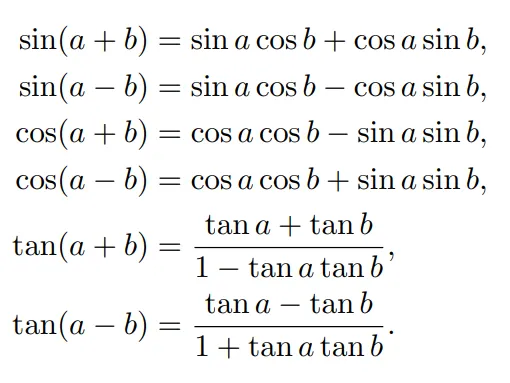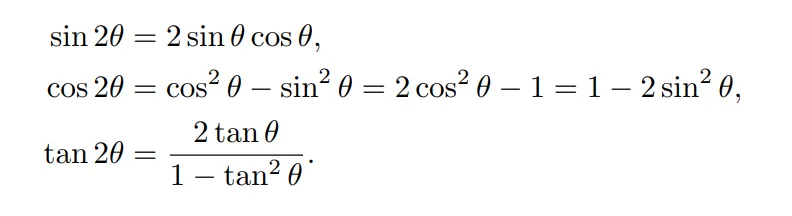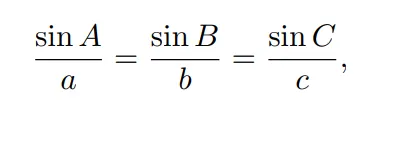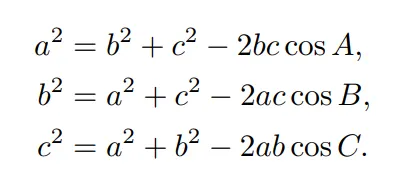앞으로 수업을 나가기전에 선형대수학 및 기하에 초점을 맞춰야 합니다. 모든걸 기초부터 설명하기는 어렵습니다. 우리도 역시 독자가 0이아닌 수준에 수학적 지식이 있다고 가정을 하고 공간수학에 집중하도록 하겠습니다. 그렇지 않으면 우리가 목표로 하는 3D 수학을 습득하는데 많은 시간이 소요될것이 때문에 빠르게 고등학교 수준의 수학을 복습해보도록 하겠습니다.
Summation and Product Notation(누적합과 누적곱)
누적합을 간단하게 표현하는 수학공식이 있습니다. 일종의 수학에서의 for 반복문을 생각하시면 됩니다.
i 는 프로그래밍에서 인덱스로 표현할수 있습니다. 기호에 위아래 있는 각 값들은 해당 수학식을 몇번 반복 할수 있는지를 확인 할수 있습니다. 위 식에서는 1 ~ 6 까지로 총 6번이 반복됩니다.
해당 식에 1부터 6까지의 값을 넣어준 결과를 누적해서 더해주는 연산입니다.
위 기호를 시그마라고도 표현하기도 합니다.
비슷한 방식의 누적곱 연산으로 아래와 같은 기호도 존재합니다. 아래 기호는 파이라고 부르기도 합니다.
Interval Notation (구간 표기법)
게임 프로그래밍 에서 우리는 때때로 간격을 표기해야 하는 경우가 생깁니다.
[-3, 2] 를 부등식으로 표현하면 -3 ≤ x ≤ -2 가 됩니다. 구간에서 시작과 끝을 제외하는 경우에는 소괄호로 표현합니다. (-1, 4) : -1 < x < 4
그외 무한대와 관련된 부등식등 다음과 같이 표현이 가능합니다.
(x, y)는 또한 점을 표현할때도 사용할수 있고 [x, y]도 벡터를 표현할떄 사용할수도 있기 때문에 우리는 점(dot, position)과 벡터(vector)에 표현방법과 명확하게 분리할 필요가 있습니다.
Angles, Degrees, and Radians(각도, 디그리, 라디안)
Angle(각도)는 회전을 표현하기 위한 양을 나타낸다.
각도는 그리스 기호 로 표현 하기도 합니다. 각도에 있어서 중요한 점은 Degree 각도와 Radian각도의 차이를 알고 이해해야 합니다. 우리는 통상적으로 우리에게 조금 더 친숙한 Degree각도를 사용합니다. 는 원에서 만큼 회전한것을 의미합니다. 이를 Radian 으로 표현 할수 있어야 합니다.
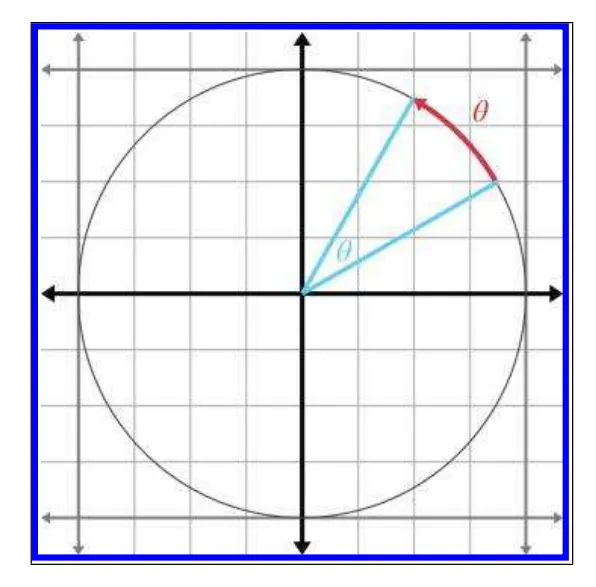
우리는 두직선을 이용해서 원에서의 회전을 표현 해보도록 하겠습니다.
두직선 사이의 각을 라디안으로 표현 해보겠습니다. 반지름이 1인 원을 기준으로 한직선에서 만큼 회전한 두번째 직선 사이의 호의 길이를 라디안이라고 합니다.
여기서 원의 둘레의 길이를 라고 합니다. 는 3.14159265359…의 무리수로 표현합니다.
그럼으로 , 의 회전으로 표현이 가능합니다.
Radian 을 Degree각도로 변환을 한번 해보겠습니다.
그때 그때 구해서 사용할 수도 있지만 자주 사용하는 값들은 한번 기억 해두는게 편하다.
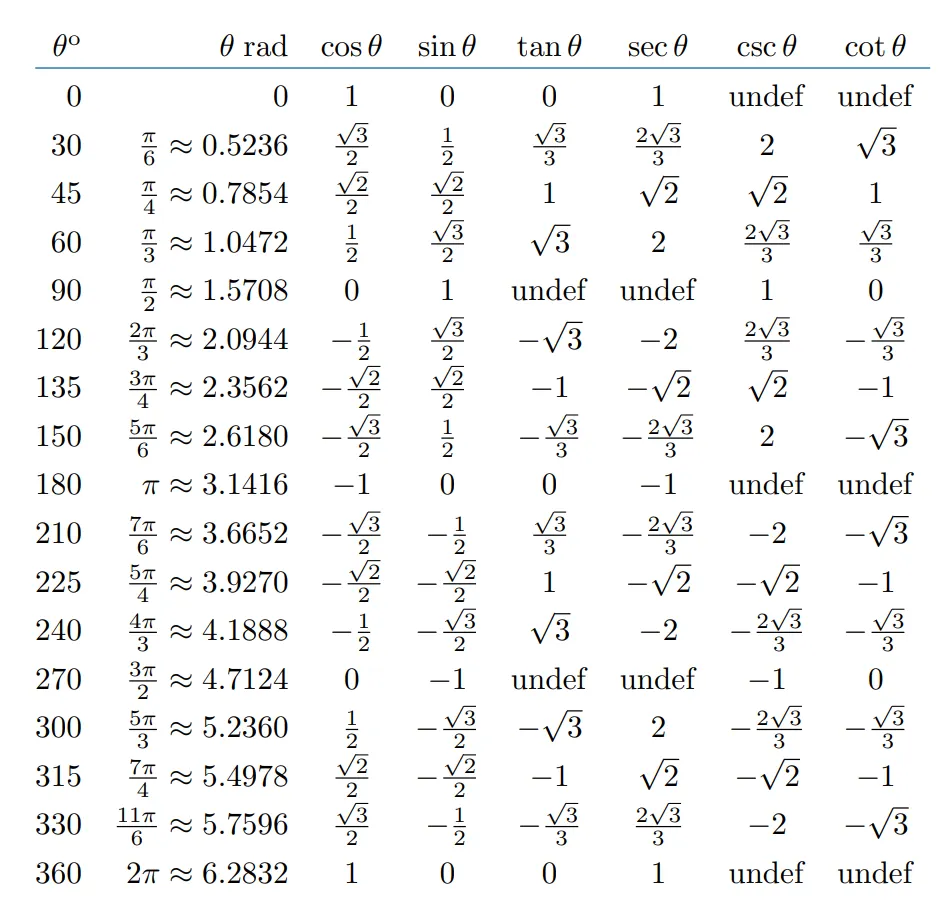
Trig Function(삼각함수)
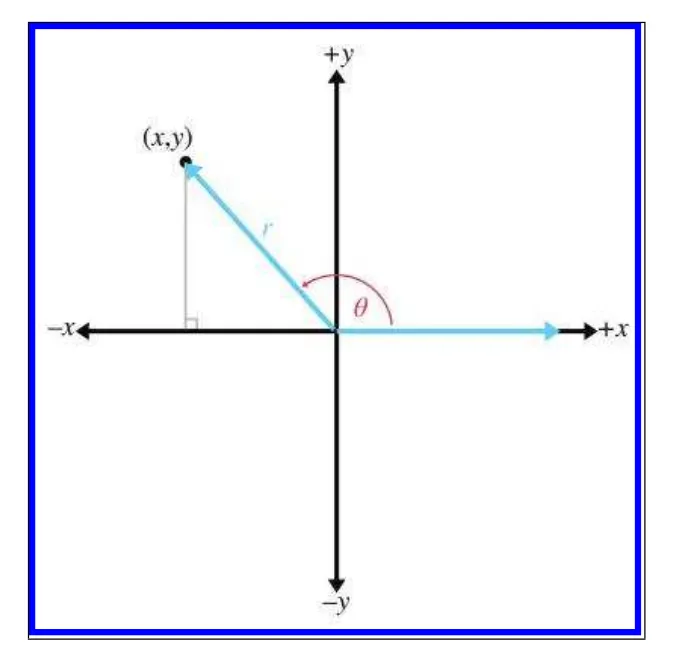
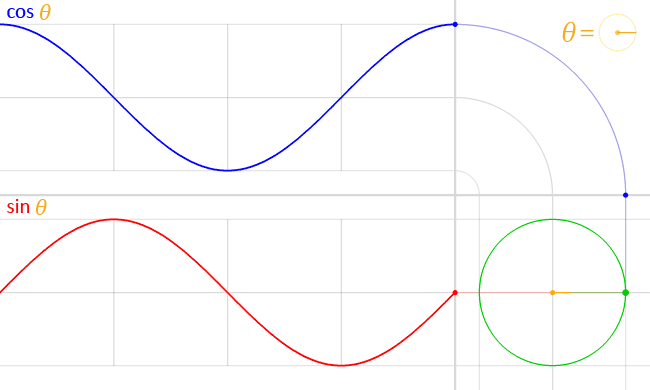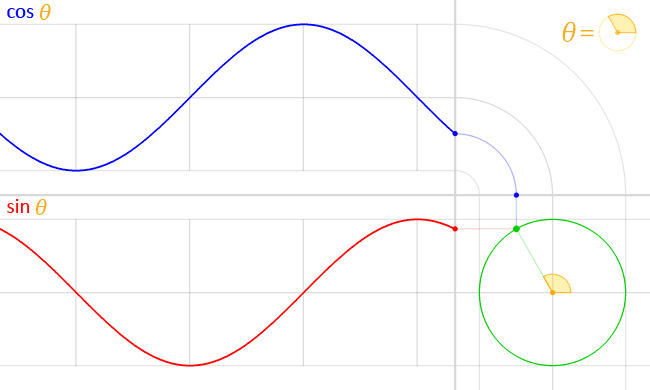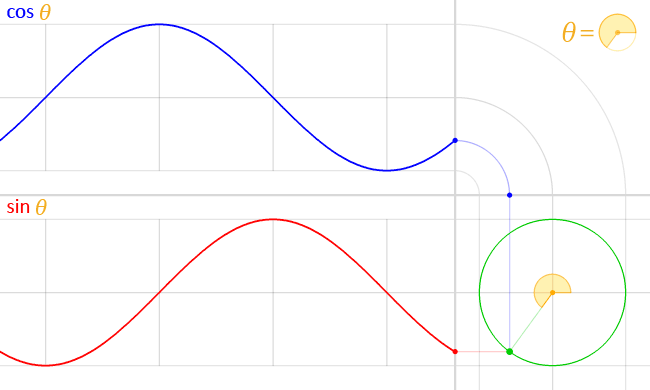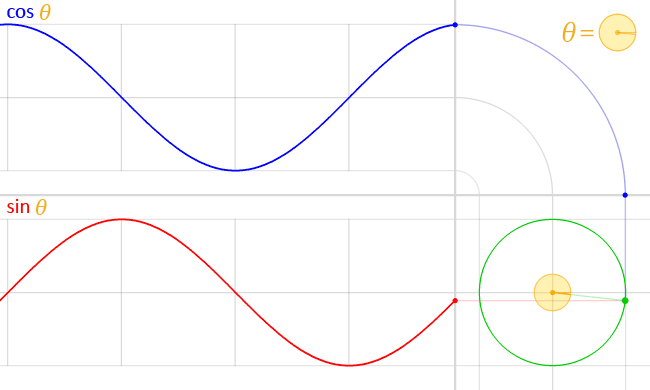
삼각함수를 정의하는 방법은 다양하게 있습니다. 우리는 단위원(반지름이 1인 원)을 이용해서 삼각함수를 정의할 것입니다.
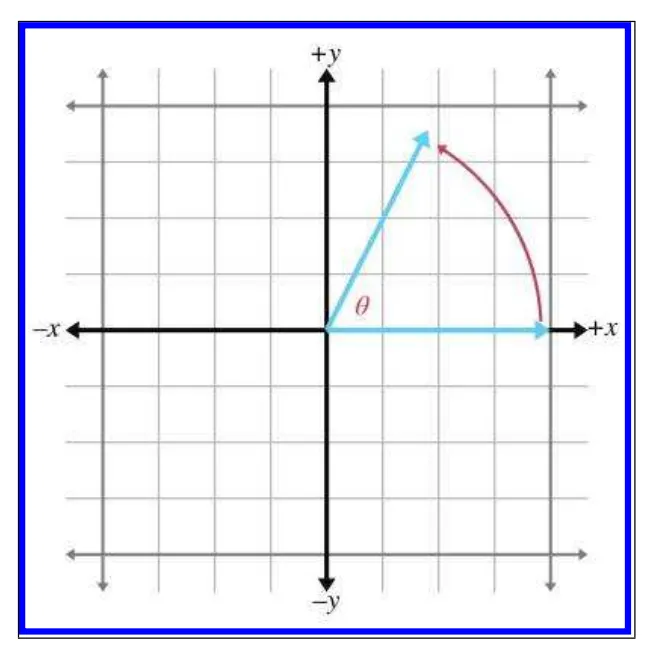
+x 방향으로 직선을 하나 그리겠습니다. 그리고 이 직선을 반시계 반향으로 만큼 회전시키겠습니다. 이는 다음 그림과 같이 그릴수 있습니다.
이 두직선을 이용해 특별한 함수를 표현 할 수 있습니다. 잘 아시다시피 cosine, sin 입니다.
그외로 sec, tan, csc, cot등이 있습니다. 이것들은 cos,sin을 이용해서 표현이 가능합니다.
위 그림에서 그려서 표현하자면 다음과 같은 그림이 됩니다.
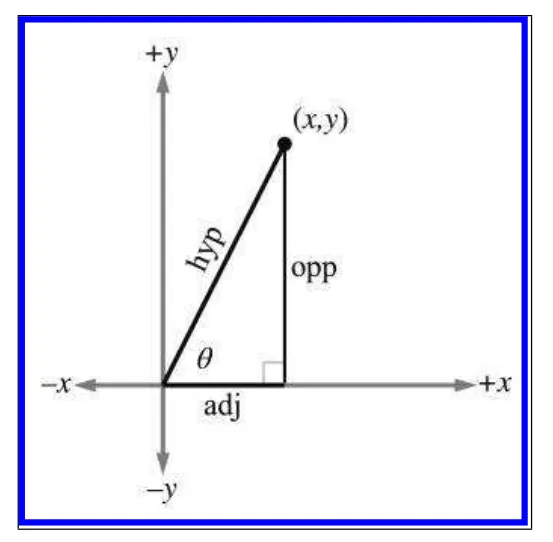
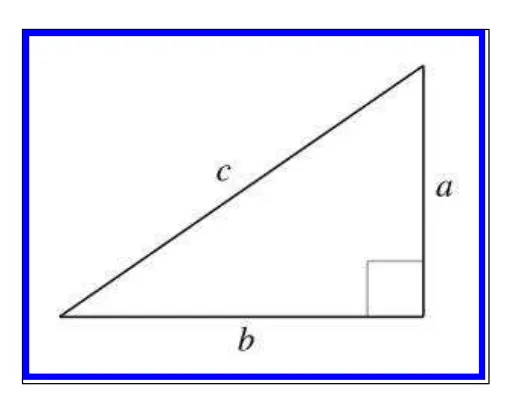
삼각함수는 다음과 같은 직각삼각형에서의 비율로 표현이 가능합니다.
이들은 직각삼각형의 특성으로 hypotenuse(빗변)이 단위길이가 아닌경우에도 적용됩니다.
하지만 이는 가 둔각(90~180)일때는 적용되지 않습니다.
둔각일때는 해당 점으로 직각삼각형을 그리기가 어렵습니다. 하지만 우리는 반지름과 x,y를 이용해 삼각함수를 표현 할수 있습니다.
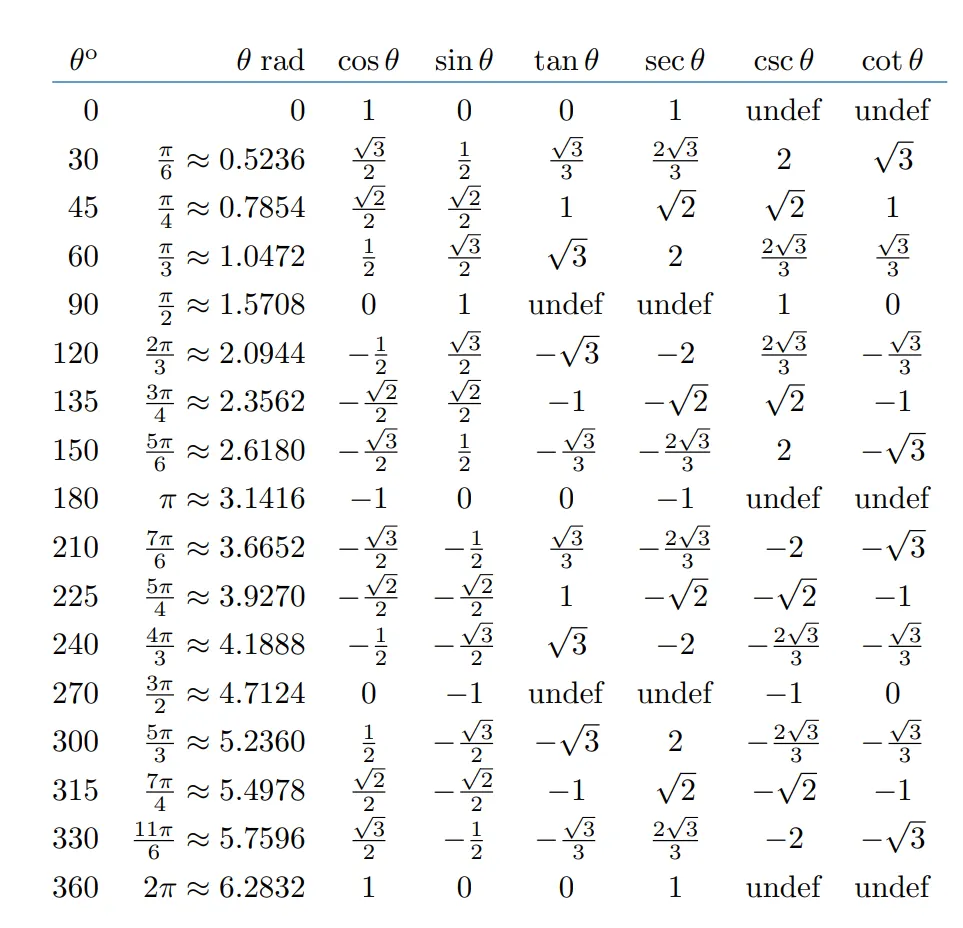
이에 우리는 삼각함수간에 여러가지 관계를 표로 만들어 볼수 있습니다. 기본적으로 여러분들이 삼각함수에 대한 사전지식이 있다고 생각하고 있기때문에 증명같은 부분은 다른 온라인 강의나, 여러매체를 통해서 찾아 볼수 있습니다.
나머지 필요한 공식들은 다음과 같이 정리 할 수 있습니다.
대부분의 사람들이 기초교육으로 받은 삼각형 공식은 피타고라스의 정리 일것 입니다.
피타고라스의 정리는 직각삼각형에서 높이와 밑변을 알면 빗변에 대한 길이를 구할수 있는 공식입니다.
공식은 다음과 같습니다.
피타고라스의 정리를 단위원에 적용시키면 다음과 같은 공식도 유도 할수 있습니다.
삼각함수의 합차 공식
삼각함수의 2배각 공식
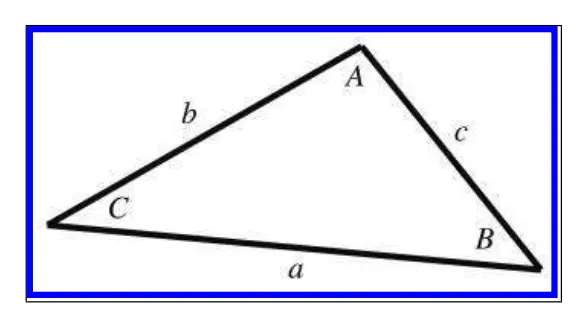
그리고 우리는 종종 알수없는 변의 길이, 각도 등등의 문제를 해결해야 할때가 많습니다. 사인,코사인 법칙을 활용하여 이러한 문제를 해결 할 수 있습니다. 그리고 항등식은 직각삼각형 분만 아니라 모든 삼각형에 적용될수 있습니다.