1D Mathmatics(수학)
Naturla Number(자연수)
1,2,3…와 같이 나아가는, 보통 대상의 개수를 셀 때 나오는 수입니다.
자연수의 집함은 영어 natrual number의 첫 글자를 따 N또는 정수의 양수 부분을 뜻하는 Z+라고 씁니다.
자연수는 물건을 세어서 기록을 하려다보니 나온 숫자입니다. 인류 초기에는 숫자의 개념이 없기 때문에 그림으로 표현을 했습니다.
어떠한 물건을 세는 것이 수학의 출발이니 만큼, 수학의 탄생을 상징하는 기본적인 개념입니다.
자연수는 너무 자연스럽게 우리 일상 생활에서 사용되기 때문에 사실적 개념으로 받아들일 수도 있지만 사실 추상화로 발명된 개념입니다.
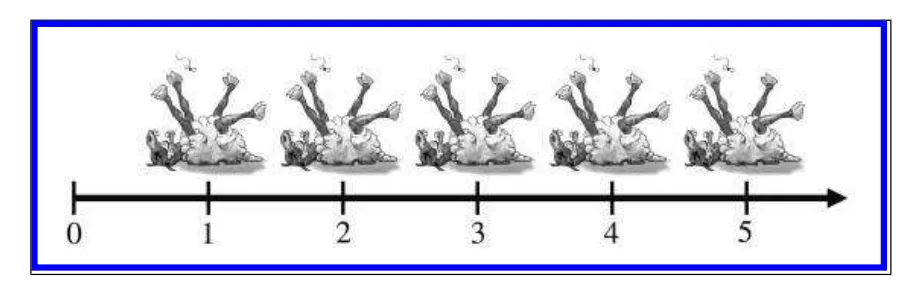
좌표와 함께 표현하면 다음과 같이 표현할 수 있습니다.
양을 한마리, 두마리, 세마리 세어나가면서 좌표에서의 위치 또는 갯수 또한 표현이 가능한 수 체계입니다.
Integers(정수)
자연수를 조금 더 확장 시키면 정수로 표현 할 수 있습니다. 역사에 어느 시점에서 실제로 소유하지 않은 양을 팔 수 있다는 사실을 알게 되었습니다. (부채, 빈곤, 대출, 담보)같은 개념이죠.
그래서 negative number(음수)를 발견하게 되었습니다.
시간이 지나면서 사람들은 양을 더 작은 단위로 나눌 필요가 있었습니다. 예를들어 “3.1415 ”, “31415 / 10000” 같은 숫자들이죠.
수학자들은 이러한 숫자를 rational number(유리수) 라고 이야기 했습니다.
얼마지 지나지 않아 일상생활에서 흔히 볼수 있는 숫자중에 유리수로 표현이 없는 숫자를 발견하게 되었습니다. 대표적인 예로는 PI(3.141592….) 원주율이었죠.
이를 Irational numbers(무리수) 라고 불렀습니다.
현실세계는 매우 불연속적 입니다. 그럼에도 수학에서는 무한한 수학이 아닌 유한한 수학 연속수학(continus mathmatics)을 사용합니다.
바로 공학에서는 매우 유용한 도구이기 때문입니다.
2D Cartesian Space
Cartesian Space 좌표계는 2차원 네모 안에서 수학의 움직임 또는 위치를 표현한다고 보면 이해하기 쉽습니다.
우리는 알게 모르게 해당 좌표시스템을 많이 사용 해왔습니다.
집의 설계도, 축구 경기장을 위에서 바라보거나, 체스, 바둑등 Cartesian space 에 노출된적이 많습니다.
가상의 도시 Careteisan city를 상상해봅시다.
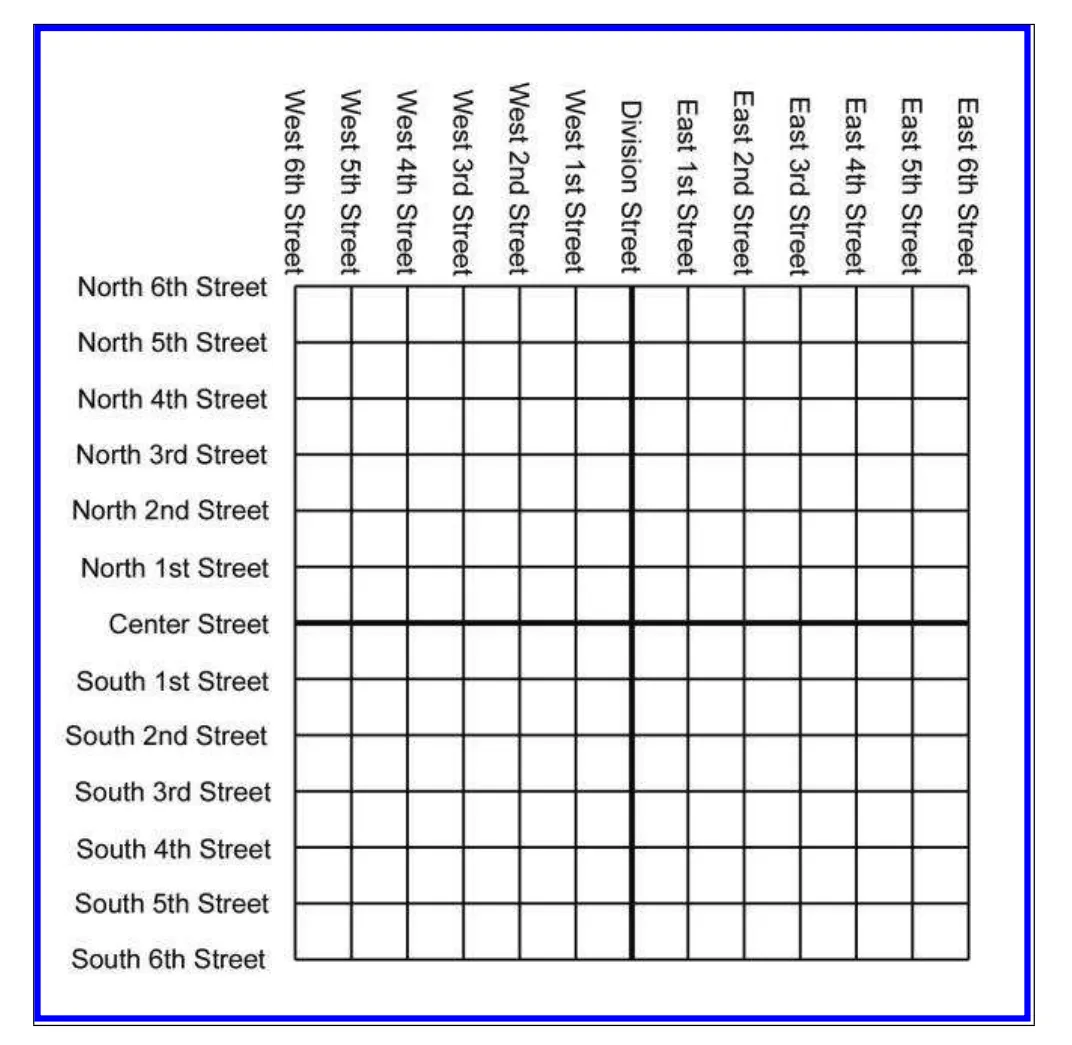
다음과 같은 도시의 지도를 사용하면
중점(Devision Street 과 Center Street의 교점) 을 기준으로 원하는 위치를 한칸씩 움직이면서 쉽게 찾아갈수 있게 됩니다. 예를들어 North 4th, West 2nd 위치에 도넛 가게가 있다면 중점을 기준으로
위쪽으로 4, 왼쪽으로 2로 이동하게 되면 찾아 갈수 있게 됩니다.
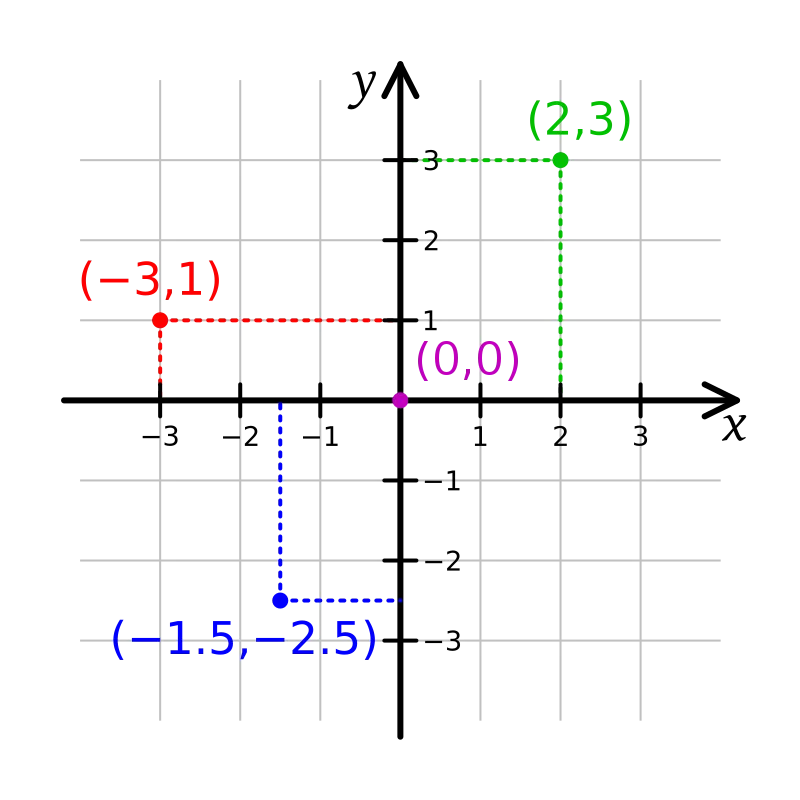
이처럼 Cartesian 좌표계를 사용하면 쉽게 위치를 표현할수 있습니다. 도시 지도를 다음과 같이 x, y, 를 이용해 좌표로 표현한 도표로 바꾸어 보겠습니다.
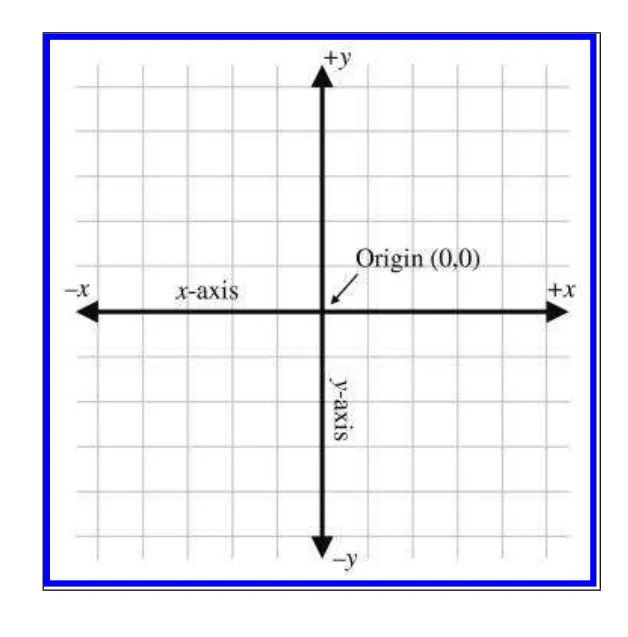
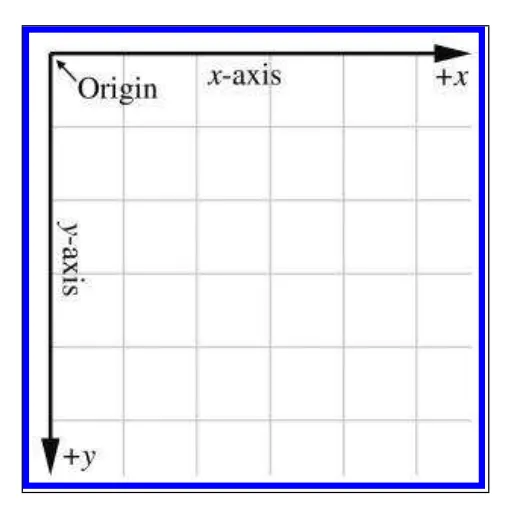
Cartesian 좌표계에선 중점(0,0) Origin이라고 합니다. 다른 말로는 Center(센터)라고도 합니다.
그리고 이 중점을 관통하는 두 선이 있습니다. 이를 x축, y축 이라고 합니다. 중점을 기준으로 위아래, 좌우로 표현이 가능하며 각각 양수와 음수로 표현이 됩니다. 또한 무한이 확장이 가능한 특성도 가지고 있습니다.
또한 항상 위아같은 형태가 아니며 한부분만 좌표계로 사용도 가능합니다.
이렇게 사용하는걸 설명하는 이유는 보통은 위와같은 좌표계를 사용하는 경우가 대다수지만
특정 영역에서 아래와 같은 좌표계를 사용하기도 합니다. 예시로(UV Texture coordinate)가 있습니다.
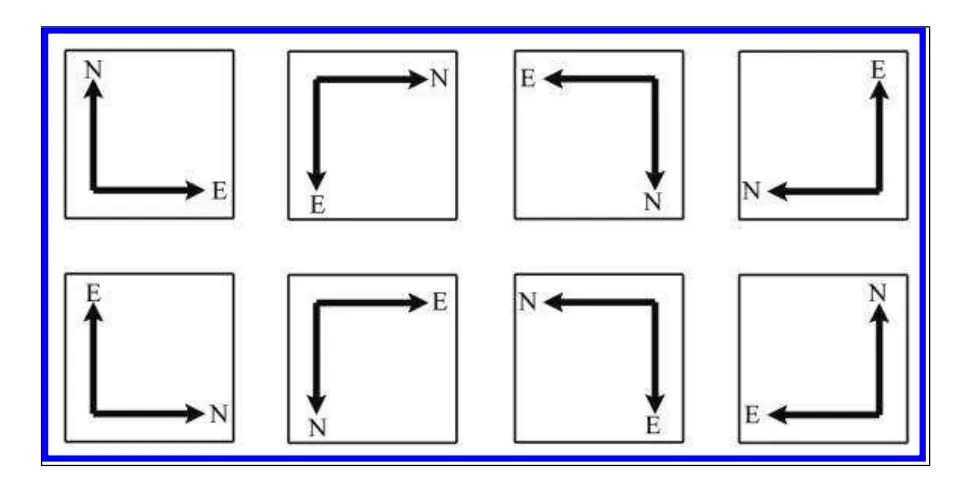
그래서 다음과 같이 총 8개의 방식으로 좌표축을 기준으로잡아 표현할수도 있습니다.
요약하자면 x축과 y축에 대해 어떤 방향을 선택하든 좌표공간을 회전하여 +x, +y를 뒤집을 수도 있고 다양하게 표현이 가능하다는 것입니다.
대표적 예시)
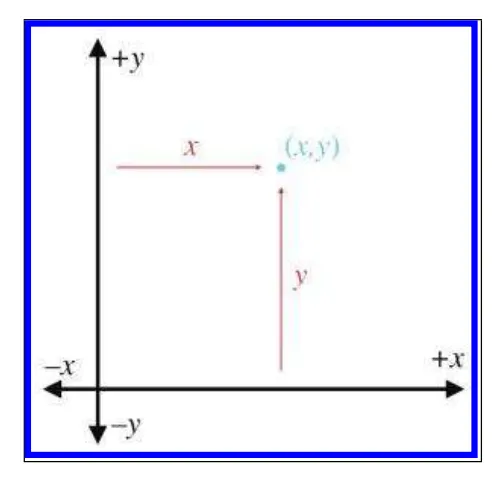
2D Cartesian 좌표계를 사용하여 위치를 정의하는 방법
좌표계는 위치를 정확하게 정의하기위한 시스템입니다. 예를들어 옜날에 지도같은게 없을 시기에 남성이 여성에게 데이트 신청을 할 때 위치를 가르켜주기 위한 시스템으로 시작되었습니다.
x,y 의 위치에서 만난다면 중점 (0,0) 을 기준으로 x만틈 이동한후에 y만큼 이동해서 해당위치를 찾아갈수 있다.
이는 2차원 공간에서의 표현 방법이고 3D공간에서는 x,y,z로 3가지의 방향을 표현 할 수도 있다.
하나의 좌표계안에서 다양한 위치를 여러개도 표현 가능 합니다.
3D Cartesian space
이제 평면 공간을 떠날 때가 되었습니다. 그리고 3D 공간에 대해서 생각해봅시다.
3D 공간은 2D보다 25~50% 정도만 복잡성을 추가 되는 것처럼 보입니다.
눈으로 보기에는 3D는 한개의 방향만 더 추가 되면 됩니다.
불행하게도 이는 사실과 많이 다릅니다. 3D 공간은 2D공간보다 더 복잡합니다. 단순히 한차원의 추가의 문제가 아닙니다. 2D에서 간단하게 해결하는 경우도 3D에선 복잡하게 해결하는 경우가 많습니다.
Extra Dimension, Extra Axis
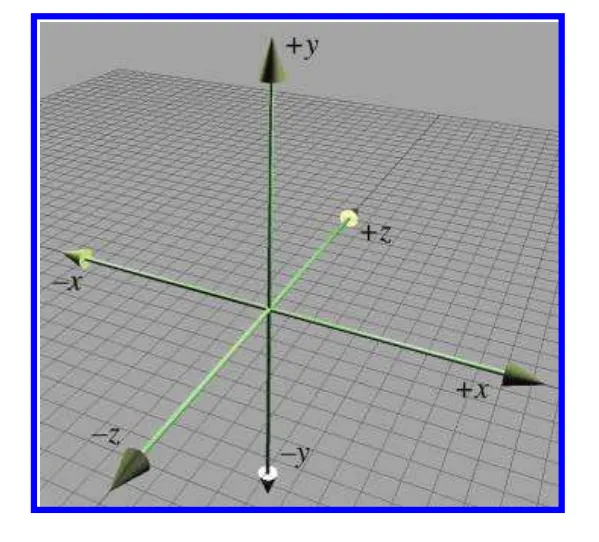
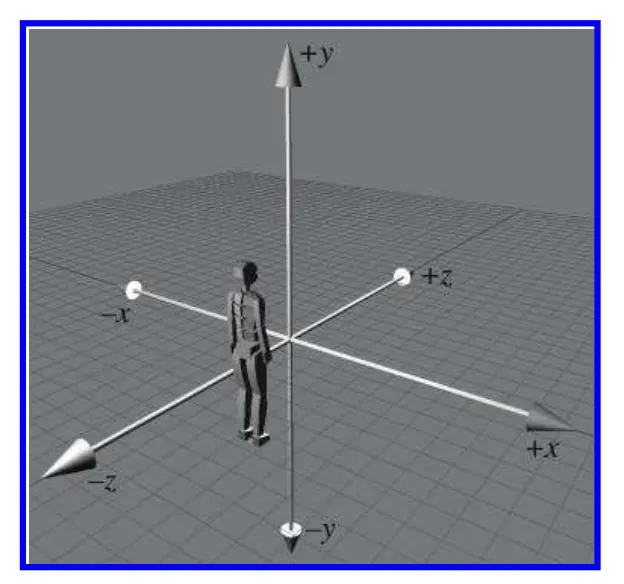
3차원에서는 3개의 축이 사용됩니다. 기본적으로 2D 에서 사용되는 x축, y축이 사용되고 z축 이 추가됩니다. 모든 축은 상호간에 수직을 이룹니다. 아래 그림과 같습니다.
+x 방향은 우리는 Right방향, +y 방향은 우리는 Up방향, +z 방향은 Foward방향으로 이야기 할 수 있다.
3D 에서 위치 정하기
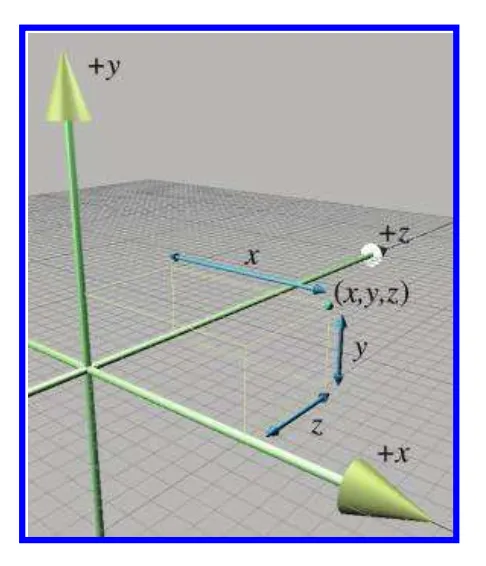
3차원에서는 3개의 숫자를 가지고 좌표를 지정합니다. x, y, z 입니다.
각각 x 좌표는 yz평면에서의 거리, y좌표는 xz평면에서의 거리, z좌표는 xy평면에서의 거리를 표현합니다. 이를 그림으로 표현하면 다음과 같습니다.
다양한 방법으로 x,y,z의 좌표를 표현 할수 있지만 이를 꼭 정확하게 정의할 필요는 없습니다.
이는 오히려 혼동을 줄수 있습니다. 단지 2D에서 하나의 z좌표를 추가함으로써 3D로 확장되었단 것을 생각해주세요.
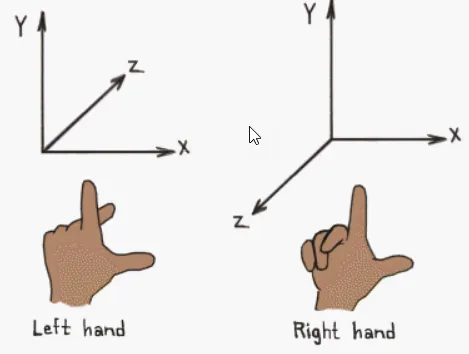
왼손좌표계와 오른손 좌표계( Left-handed versus Right-handed Coordinate Spaces )
2D 좌표계에서는 모든 좌표계 시스템이 동일한 좌표계 시스템을 사용하는 경우가 대다수 입니다.
하지만 3D에서는 다른 좌표계를 사용하는 경우가 많습니다.
기존에 +z 가 foward방향을 가르키고 있지만 이를 뒤집을 수도 있습니다.
즉 모든 3차원 좌표공간은 좌표 시스템이 동일하지 않을수 있다는 이야기입니다. 결국 물체를 x축으로 회전 시킨다고 표현 할때 결과가 달라 질 수 있습니다.
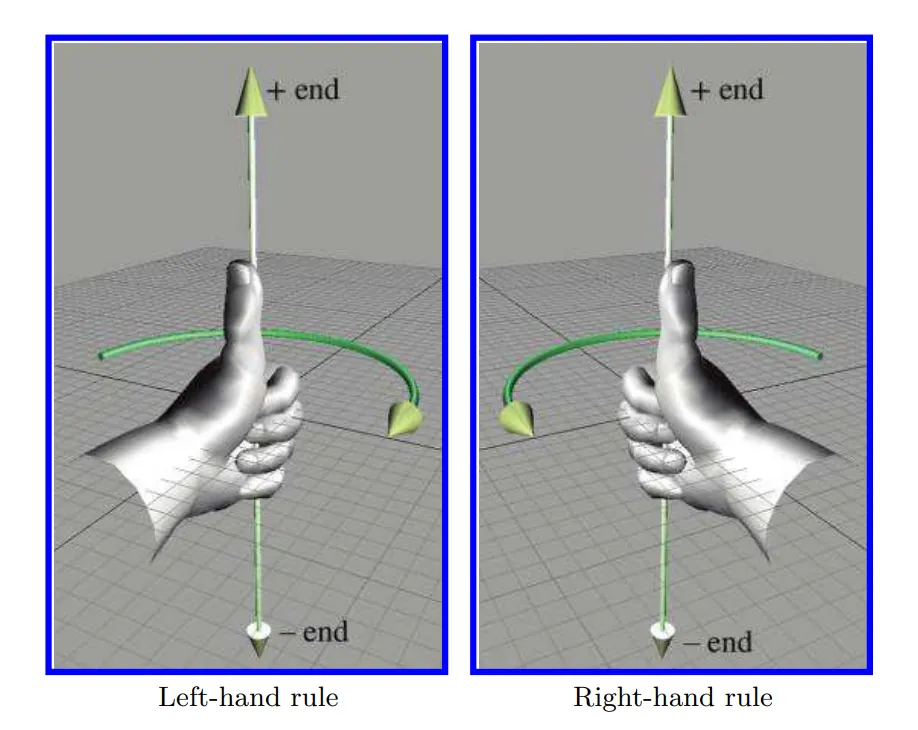
.왼손 좌표계와 오른손 좌표께는 “양의값으로 회전” 시켯을때 대한 정의가 다릅니다. 즉 회전 방향 또는 결과가 아예 달라질수 있다는 이야기입니다.
+30도로 회전한다고 가정했을때
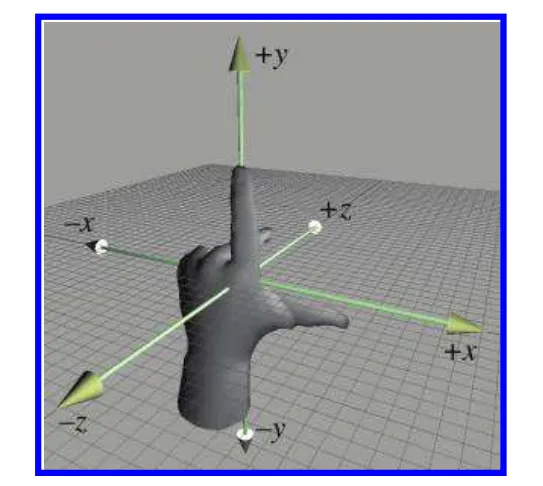
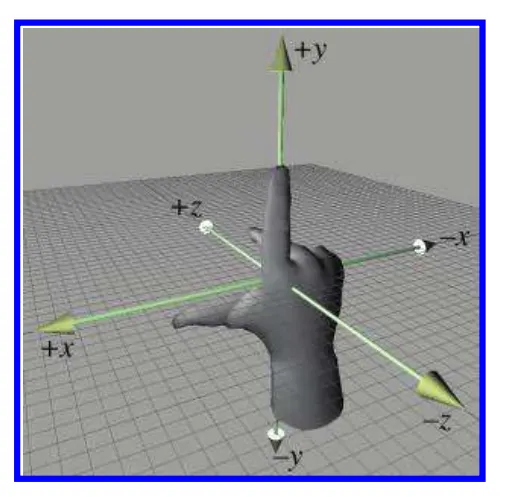
z축의 방향이 뒤집혀 있기때문에 위 그림과 같이 서로다른 좌표계에서는 반대쪽 방향으로 회전할수 있습니다. 왼손좌표계에서는 왼손을 들고 엄지를 세운후 손가락쪽으로 회전시키는걸 양의 방향으로 정해두었습니다. 오른손 좌표계에서는 양의 회전방향이 오른손 기준으로 손가락쪽 방향이기 때문에 반대 방향입니다.
양쪽 좌표계는 서로간에 변환이 가능합니다. 가장 간단한 방법은 회전축에 양수 음수 방향 교환하는 방법입니다.
다양한 분야에서 둘중에 하나를 사용합니다. 일부 최신 컴퓨터 그래픽 문헌은 왼손좌표계를 사용하는 방면, 전통적인 그래픽 문헌과 수학중심의 선형대수학에서는 오른손 좌표계를 선호하는 경향이 있습니다. 하지만 이는 개인적인 생각으로 꼭 작업전에 해당 프로세스가 어떤 좌표계를 사용하는지 미리 확인 해야 합니다.
결론적으로 위 표와 같은 방법으로 변환할수 있지만 간단하게 표현하면 z축을 뒤집으면 끝납니다.
만약에 다른 프로그램의 리소스를 불러 왔을때 제대로 보이지 않는다면 z축의 기호를 뒤집어 보시는것도 좋은 방법입니다.
다만 요즘에는 사용하는 프레임워크에 따라서 미리 정해진 경우가 많습니다. 우리는 이를 알고 주의하여 작업을 진행하면 됩니다. 우리 책에서는 위 그림과 같이 왼손 좌표계를 따르도록 하겠습니다.