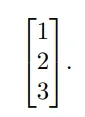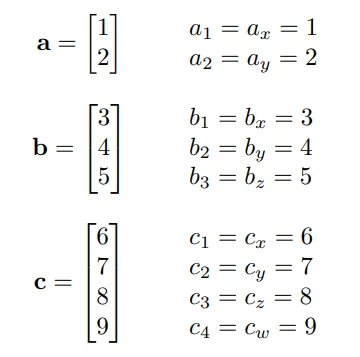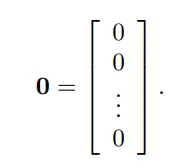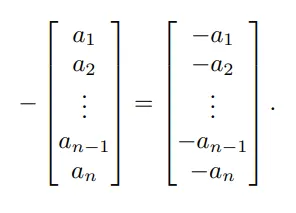벡터(Vector)는 2D, 3D수학에서 자주 사용됩니다. 벡터라는 용어는 다양한 의미로 사용됩니다.
선형대수학에서 벡터, 물리에서의 벡터, 기하학에서의 벡터, 좌표계에서의 벡터 다소 추상적이며 다양하게 사용되고 있습니다. 우리가 이 차이들을 전부 알 필요는 없지만 3D수학에서 벡터가 사용되는 2가지 경우들은 이해해야 합니다.
수학에서의 벡터는 나열된 숫자의 조합입니다. 프로그래머 기준으로 생각해 보면 배열과 가장 비슷한 구조입니다. 지금 잘 와닿지 않는다 해도 너무 걱정하지 마세요.
많은 수학적 주제들이 처음에는 익숙하지 않을 수 있습니다.
수학에서는 벡터(vector) 와 스칼라(scalar)를 구분합니다. 예를들어 속도(velocity), 변위(displacement) 등의 값은 벡터로 표현하고 속력(speed) 거리(distance)등의 값은 스칼라로 표현합니다.
벡터는 차원을 표현 할수 있습니다. 한개의 값을 사용하면 1차원 2개의 값을 사용 하면 2차원…3,4 차원 등등 하지만 스칼라는 1차원밖에 표현하지 못합니다.
벡터를 표현 할때는 배열과 같은 [] 기호를 이용하여 표현합니다.
예를들어 [1,2,3] 벡터와 같이 가로로 표현하는 경우도 있고
그림과 같이 세로로 표현하는 경우도 있습니다.
벡터의 각각원소는 벡터의 이름기호 밑에 작은숫자로 표현합니다.
여기서 보면 4D 벡터는 x,y,z,w로 구성되어있습니다. 4번쨰 원소는 w를 사용합니다.
이제 중요한점에 대해서 이야기 해보겠습니다. 우리는 스칼라와 벡터를 구분하기 위한 서체 규칙을 적용 시킬 것입니다.
스칼라를 표현 할때는 일반 서체로 표현합니다.
: a, b, x, y, z, θ, α, ω, γ
벡터를 표현 할때는 굵은 글꼴로 표현합니다.
: a, b, u, v, q, r
매트릭스를 표현할떄는 대문자와 굵은 글꼴로 표현합니다.
:A, B, M, R
진행하기에 앞서 벡터의 관점에 대해서 마무리 짓도록 하겠습니다. 벡터와 공간을 다루는 수학을 우리는 선형대수학이라고 부릅니다. 우리는 벡터를 이용하여 더 많은 문제들을 해결 할수 있습니다. 선형대수학에서 n차원의 벡터와 행렬은 어떤 값이 대입되든지 간에 신경쓰지 않고 여러가지 공간 관련된 연산을 해결 할수 있도록 도와줍니다.
우리는 게임에 관련된 기하학적 관점에 초점을 맞추어 n차원의 문제 해결에 집중하기보다, 2D,3D,4D 벡터와 행렬연산에 집중하겠습니다.
벡터의 기하학적 정의
자 이제 벡터에 관해서 논의 해봅시다. 조금더 기하학적 해석으로 접근해 봅시다. 기하학에서는 벡터는 크기와 방향이 있는 선분입니다.
•
벡터의 크기는 벡터의 길이 입니다. 벡터는 양의 길이만 가질수 있습니다.
•
벡터의 방향은 화살표를 통해 벡터가 가르키는 방향을 나타낼 수 있습니다. 여기서 우리는 Orientation과 direction을 구분할줄 알아야 합니다. 이에 대한 차이는 뒤에서 설명하도록 하겠습니다.
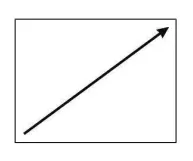
그림과 같은 벡터를 봐봅시다.
위그림은 2D화면상에서 벡터를 표현한 것입니다. 마치 화살표가 어딘가를 가르키는 모습과 같죠?
이것이 일반적인 벡터를 표현하는 방법입니다. 그림을 보면 화살표의 길이와 방향 두가지를 유추할수 있습니다.
우리가 여기서 봐야할건 벡터의 꼬리와 머리 부분입니다. 꼬리 부분이 시작되는 위치로 볼수 있고 머리(화살표)부분이 도착하는 위치로 볼수 있습니다.
그럼 벡터는 어디에 위치해 있을까요? 사실 그건 적적하지 못한 질문입니다.
벡터는 위치(position)를 가지고 있지 않습니다. 오로지 크기(magnitude)와 방향(direction)만 가지고 있습니다. 아마 이는 불가능 하다고 들릴수도 있습니다. 하지만 우리가 일상생활에서 다루는 수많은 값들도 크기와 방향은 있지만 위치는 없는 것들이 많습니다.
아래 두문장을 비교하여 이해해보세요.
•
Displacement(변위) : “세걸음 앞으로 나가보세요.” 이 문장은 취이에 관한 것 처럼 보이지만 사실 문장 자체를 보면 변위(크기)이며 절대적으로 어느 위치에 있는지 알 수 없습니다. 이러한 표현들을 벡터로 나나낼 수 있습니다.
•
Velocity(속도) : “나는 북쪽방향으로 50km/h 로 이동중 입니다.” 이 문장도 마찬가지로 시속 50km/h 크기와 북쭉방향(방향)만을 가지고 있습니다. 이 와같은 값도 벡터로 표현하기에 좋습니다.
변위(displ;acement)와 속도(velocity)는 거리(distance)와 속력(speed)와는 다릅니다.
변위와 속도는 방향을 내포하고 있습니다. 그에 반면에 거리와 속력은 방향은 없고 크기만을 내포하고 있습니다.
결론적으로 벡터는 사물 간의 변위와 상대적 차이를 표현하는데 있어서 사용됩니다.
예를들어 “우리 집읍 여기서 동쪾으로 3블록 떨어져 있어요.”
중요!! 벡터가 절대적인 위치 자체를 가지고 있다고 생각해서는 안됩니다.
길이와 방향은 중요하지만 위치는 중요하지 않습니다.
벡터에는 위치가 없기 때문에 어떤 다이어그램에서도 우리는 벡터를 표현 할 수 있습니다. 물론 우리는 종종 이러한 벡터의 성질을 이용하여 위치, 방향, 크기 등등을 구할 수도 있습니다.
자 이제 기하학점 관점에서 벡터를 살펴 봤으니 데카르트 좌표계에서의 벡터도 알아 보도록 합시다.
Specifing Vectors with Cartesian Coordinates(데카르트 좌표계에서의 벡터의 정의)
자 이제 벡터를 데카르트 좌표계로 옮겨봅시다. x축과 y축을 사용 하는 2차원 좌표계에서 벡터는 다음 그림과 같이 표현 가능 합니다.
위 그림은 2D vector를 표현합니다. 보시다시피 벡터의 시작위치는 벡터를 표현하는데 있어서 중요하지 않습니다.
아래 그림에서 [1.5, 1] 벡터 두개를 비교하면 두 벡터는 같은 위치에 있지 않습니다. 하지만 값은 같은 벡터입니다. 또한 3차원상의 벡터도 표현하기 쉽습니다. 2차원에서 z값만 추가하여 표현 하면 됩니다.
데카르트 좌표계에서만 벡터를 표현 가능한건 아닙니다. 나중에 극좌표에서도 벡터를 표현 가능합니다. 특히 물리학에서 극좌표계는 자주 사용되는 개념입니다. 극좌표계는 뒤에서 알아보도록 하겠습니다.
Vector as a Sequence of Displacements(변위와 벡터)
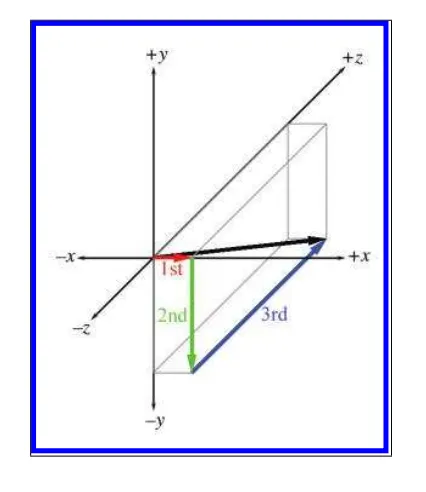
벡터로 최종 변위를 표현하는데 있어서 한가지 좋은 방법은 최종 변위를 각각의 x,y,z축의 벡터 조합으로 나누어서 표현 하는 겁니다.
예를들어 한개의 3D 벡터 [1, -3, 4]가 있습니다. 우리는 이를 각각의 x→1 만큼 y→-3만큼 z→4만큼의 벡터로 나눌수 있습니다.
x,y,z 순서는 중요하지 않습니다. 앞으로 4 아래로3 옆으로1 만큼 이동할수 있으며 세가지가 모두 결합 됬을때 동일한 변위만큼 이동합니다.
The Zero Vector(영 벡터)
주어진 차원에서 모든 위치에 0에 있는 벡터 영벡터라고 하는 특수 벡터가 있습니다.
0벡터는 특별합니다. 이는 크기가 0인 유일한 벡터이기 떄문입니다. 영벡터 이외에 벡터는 전부 크기가 양수로 되어있습니다. 그리고 0벡터는 유일하게 방향을 나타낼수 없는 벡터입니다.
이에 따라서 0벡터는 화살표로 벡터를 그리거나 표현할수 없습니다.
우리는 대신 0벡터를 화살표 대신에 점(dot)으로 표현합니다. 다만 주의할점이 있습니다.
점이라고 해서 0 벡터가 위치를 표현하는것은 절대 아니라는 것입니다.
스칼라에서 0은 수량(양)이 없음으로 표현되는 것처럼 0벡터도 “변위 없음”으로 표현하면 됩니다.
또한 제로벡터는 덧셈연산에 대한 항등식입니다. 항등식이란 해당 연산을 진행해도 자기 자신의 기존값이 그대로 나오는 결과에 따른 식을 항등식이라고 합니다.
스칼라에서 0 + x = x 가 되는 것처럼 zero_vector + other-vector = other-vector가 됩니다.
벡터(vector)와 점(point)의 비교
point(점)은 위치를 가지고 있습니다. 하지만 길이나 두께에 대한 정보는 아예 없습니다.
우리는 앞장에서 벡터가 어떻게 크기와 방향을 갖는지 학습했습니다. 하지만 위치(position)는 가지고 있지 않습니다. 그래서 위치와 벡터는 서로 다른 목적성을 가지고 있는걸 알 수 있습니다.
개념적으로 표현하자면 점(point)는 위치(position), 벡터(vector)는 변위(displacement)를 표현 합니다.
점과 벡터는 강한 관계를 유지하고 있습니다. 우리는 이장에서 이점에 대해서 학습할 예정입니다.
Relative Position(상대적인 위치)
벡터는 변위만 표현 가능합니다. 벡터는 상대적 위치를 표현 할 수 없습니다.
그럼 어떻게 상대 위치를 표현 할 수 있을 까요?
위치를 표현 할떄는 시작(기준)좌표를 기준으로 그것으로 부터 어디에 있는지를 설명해서 표현 가능합니다.
그럼 우리는 위 문장에서 몇가지 궁금점을 가질수 있습니다.
1.
위치는 어디에 있습니까?
2.
절대적 위치란 어디입니까?
위치 좌표를 나타내는 숫자만으로 위 질문에 대한 대답을 내릴 수 없다는건 매우 신기한 사실입니다.
위치라는 용어를 정의 하기 위해서는 약속되어 있는 일부 분야 안에서만 정의 할 수 있습니다.
예를들어 지리좌표계 (Geographic Coordinate System)에서 위도,경도 등을 사용하여 지구 상의 위치를 표현하는 좌표계가 대표적입니다.
반대로는 우주 공간 에서는 기준이 없기 떄문에 절대좌표라는 개념이 없습니다.
The Relationship between Points and Vectors(포인트와 벡터의 상관관계)
벡터는 변위를 표현하는데 사용됩니다. 그럼으로 벡터는 상대위치를 표현하는데 적합합니다. 포인트는 특정 좌표(위치)를 표현합니다. 하지만 우리는 위치를 지정하는 방법은 결국 상대적이어야 표현 가능하다는 것을 배웠습니다. 그럼으로 포인트도 상대적이라는 결론이 나옵니다.
포인트는 원점을 기준으로 표현되는 상대적 좌표로 볼수 있습니다. 이것이 포인터와 벡터의 상관관계 입니다.
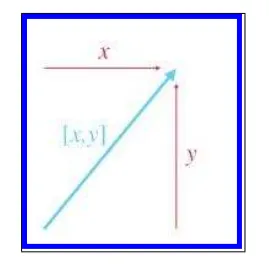
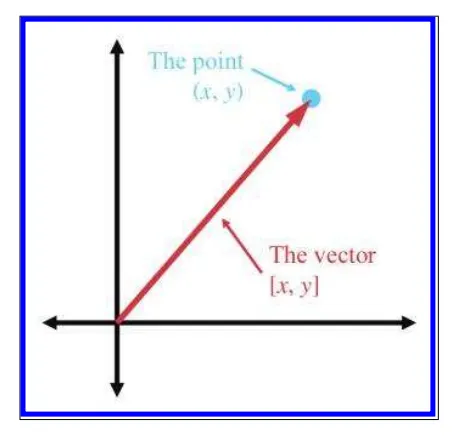
그림을 보면 원점(0,0)에서 얼마만큼의 양이 이동했는지를 나타내는 것이 벡터[x,y] 그 도착지점이 포인트(x, y) 로 표현 됩니다.
이는 결과적으로 보면 다른것처럼 느껴질수 있지만 점과 벡터는 개념적으로 구별 되야 한다는것을 이해하는것이 매우 중요합니다.
“점” 과 “벡터” 사이의 이러한 혼동 떄문에 처음에 게임수학을 학습하는데 있어서 어려움을 느겼을 것입니다. 하지만 이제 여러분들에게는 큰 걸림돌이 아닐것 입니다.
위치를 생각 할때 포인트(point)를 생각하고 점(dot)을 찍어 시각화 하고
변위(displacement)를 생각할때는 벡터(vector)를 생각하고 화살표(arrow)로 시각화 하면 됩니다.
대부분의 경우에는 변위는 원점(0,0)에서 발생하는 경우가 많아서 점과 벡터의 구분이 비슷하다고 착각 할수 있습니다.
하지만 우리는 원점에 관계없이 양과 방향을 처리하는 경우가 있습니다. 이러한 경우에는 점이 아닌 화살표로 시각화 하는 것이 중요합니다.
또한 점은 원점을 기준으로 표현하는 벡터의 도착지로 표현이 가능합니다. 즉 벡터로도 표현이 가능하다는 것이죠.
사실 많은 사람들은 벡터와 점을 수학적으로 동등하게 취급하는 이 문제 대해서 확고한 입장을 취하고 있습니다. 결론적으로 이 둘은 매우 다르며 동등하게 생각하지 말아야 합니다.
앞으로 우리는 최대한 이 둘을 구분해서 사용하려고 하겠지만 상황에 따라서 가끔 구분되지 않을떄도 있습니다. 이점 유의해주시기 바랍니다.
It’s All relative
벡터 연산을 하기전에 잠시 휴식을 가져보도록 하겠습니다. 일상생활에서 사용되는 대부분의 수치들은 절대적으로 표현하기 매우 어렵습니다. 그래서 우리는 상대적인것들 사용합니다.
Temperature(온도), Loudness(소음), Velocity(속도)등이 있습니다.
Negating a vector(음 벡터)
이번 섹션에서는 벡터에 대한 다른 수준의 이해를 해보겠습니다.
벡터에 대한 여러가지 연산을 살펴보겠습니다. 먼저 수학적인 공식을 정의하고 기하학에서의 해석을 설명한 후에 사용예를 살펴 보도록 하겠습니다.
첫번쨰는 벡터의 음의 작업입니다. 우리가 zero벡터에 대해서 이야기 할때 우리는 제로벡터를 덧셈에 대한 항등식으로 표현 했습니다.
다시 뒤로 돌아가서 특정 특정 벡터에 어떤 값을 더해주면 제로벡터가 되는 식을 구할수 있을까요?
대부분의 경우 -x 에 +x 를 더할떄 덧셈 항등식(0)을 생성하는 요소가 됩니다.
x + (-x) = 0 이 연산을 벡터에도 적용 시킬수 있습니다. V + (-V) = 0
Official Linear Algebra Rules (선형대수학의 규칙)
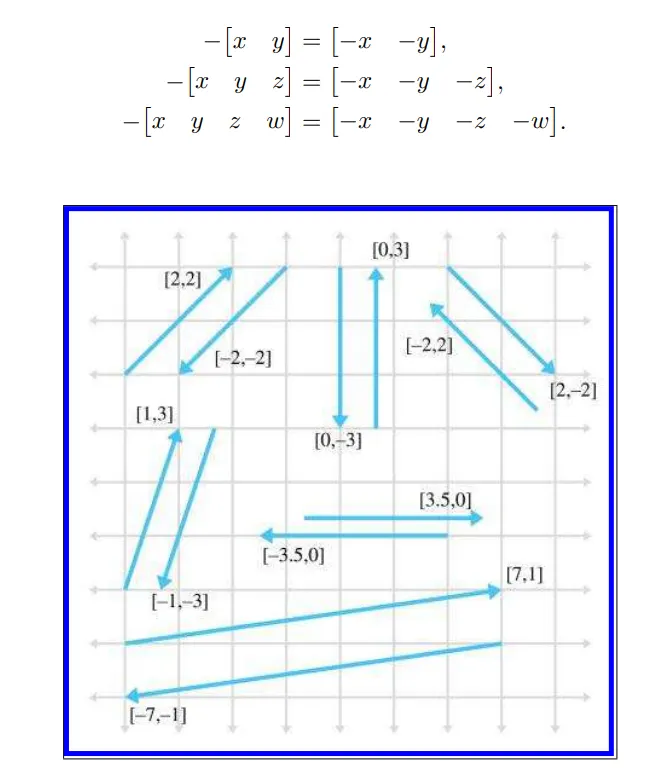
음의 벡터를 표현하는 방법은 각 벡터의 구성요소에 음수만 적용 시켜주면 됩니다.
2D,3D,4D에도 똑같습니다. 대신 화살표의 방향은 180도 회전을 한 반대방향을 가르키고 있을것 입니다. 다시한번 강조하지만 벡터에서 위치는 중요하지 않으며 크기와 방향만을 참고하시면 됩니다.