트리 탐색 및 미로찾기 수업노트
길찾기 알고리즘을 배우기 전에
길찾기 알고리즘을 배우기 전에 기초에 트리 그래프 등등을 재귀함수를 이용하여 순회 했던 방식들을 복습해보자!
기초에 배웠던 Tree 탐색 방법(2진트리 1차원 배열 기준) 다음과 같은 재귀함수를 활용해 순회가 가능하다.
트리 배열 표현
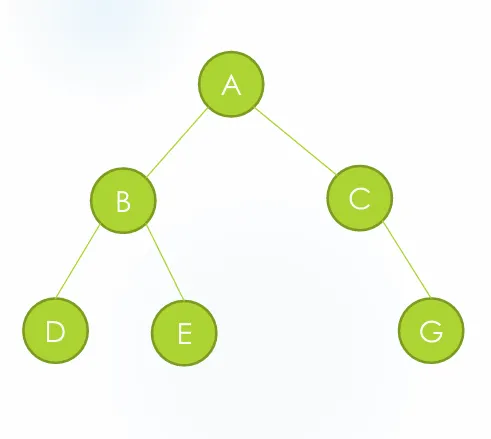
트리 구조: A-B(D,E), A-C(G)
배열 인덱스: [-, A, B, C, D, E, -, G]
#include <stdio.h>
char data[10] = "_ABCDE_G";
int n = 7;
void dfs(int level, int nowIndex)
{
if (nowIndex > n || data[nowIndex] == '_')
{
return;
}
int t;
int next;
for (t = 0; t < 2; t++)
{
next = nowIndex * 2 + t;
dfs(level + 1, next);
}
}
int main()
{
dfs(0, 1);
return 0;
}
C++
복사
하지만 위 방식은 단점이 존재한다. 의도치 않은 마지막 노드에서 한꺼제 더 진입한후 나오는 불필요한 스택면상이 사용되게 된다.
이방식을 보완해주려면 조건문을 재귀함수 호출전에 이용해서 보완이 가능하다.
전위, 중위, 후위 순회
담색하는 순서대로 노드를 출력하고 있다 (전위 순회)
#include <iostream>
char tree[256] = { 0, 'A', 'B', 'C','D','E', 0, 'G'};
int n = 7;
void dfs(int level, int nowIdx)
{
int left = nowIdx * 2;
int right = nowIdx * 2 + 1;
std::cout << tree[nowIdx] << " ";
if (left <= n && tree[left] != 0)
{
dfs(level + 1, left);
}
if (right <= n && tree[right] != 0)
{
dfs(level + 1, right);
}
}
int main()
{
dfs(0, 1);
return 0;
}
C++
복사
마지막 노드만 출력하기 (중위순회)
#include <iostream>
char tree[256] = { 0, 'A', 'B', 'C','D','E', 0, 'G'};
int n = 7;
void dfs(int level, int nowIdx)
{
int left = nowIdx * 2;
int right = nowIdx * 2 + 1;
if (left <= n && tree[left] != 0)
{
dfs(level + 1, left);
}
std::cout << tree[nowIdx] << " ";
if (right <= n && tree[right] != 0)
{
dfs(level + 1, right);
}
}
int main()
{
dfs(0, 1);
return 0;
}
C++
복사
마지막 노드 도착했을때 경로 출력하기(후위순회)
#include <iostream>
char tree[256] = { 0, 'A', 'B', 'C','D','E', 0, 'G'};
int n = 7;
void dfs(int level, int nowIdx)
{
int left = nowIdx * 2;
int right = nowIdx * 2 + 1;
if (left <= n && tree[left] != 0)
{
dfs(level + 1, left);
}
if (right <= n && tree[right] != 0)
{
dfs(level + 1, right);
}
std::cout << tree[nowIdx] << " ";
}
int main()
{
dfs(0, 1);
return 0;
}
C++
복사
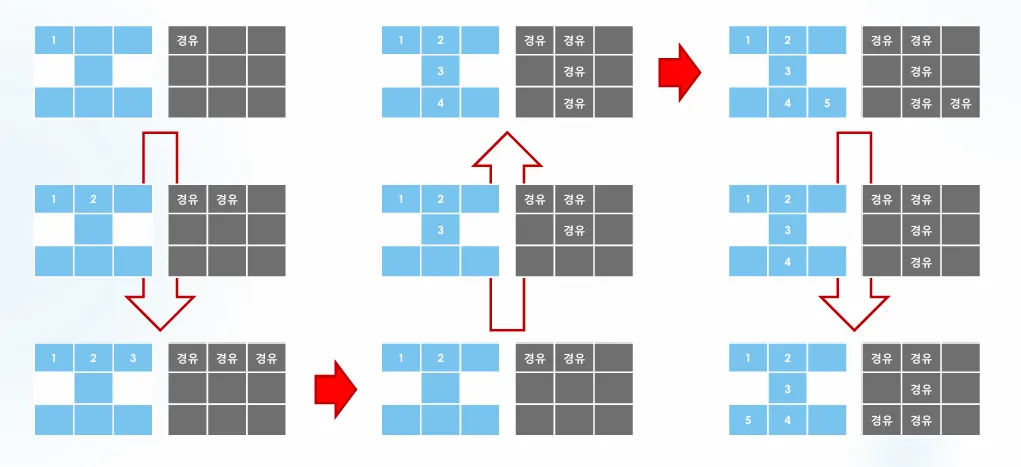
마지막 노드 도착했을때 경로 출력하기
char value[6] = "TBECD";
char path[6] = "";
int map[5][5] =
{
0,1,1,0,0,
0,0,0,1,1,
0,0,0,0,0,
0,0,0,0,0,
0,0,0,0,0,
};
void run(int now, int level)
{
std::cout << value[now];
for (size_t i = 0; i < 5; i++)
{
if (map[now][i] == 1)
{
path[level + 1] = value[i];
run(i, level + 1);
path[level + 1] = 0;
}
}
}
int main()
{
path[0] = 'T';
run(0, 0);
}
C++
복사
인접행렬로 이루어진 트리 탐색하기
#include <iostream>
#include <map>
char data[10] = "ABCDEG";
int tree[6][6] = {
{0, 1, 1, 0, 0, 0},
{0, 0, 0, 1, 1, 0},
{0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0}
};
//int n = 6;
void dfs(int level, int now)
{
std::cout << data[now];
for (int i = 0; i < 6; i++)
{
if (tree[now][i] == 1)
{
dfs(level + 1, i);
}
}
}
int main()
{
dfs(0, 0);
return 0;
}
//DFS 복습 해보기
//트리일때 (1차원 배열일때)
// 인접행렬일때
// 그래프 DFS (복습해보기)
C++
복사
미로찾기
기본 개념
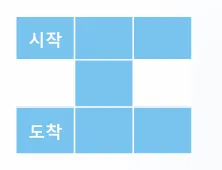
시작지점에서 도착지점까지 가는 경로를 알아내는 문제
기존에 우리가 배웠던 DFS 알고리즘을 이용해서 길찾기를 해볼 생각이다.
기존에는 DFS 알고리즘, 재귀함수를 이용하여 경로수를 모두탐색하는 방식이다.
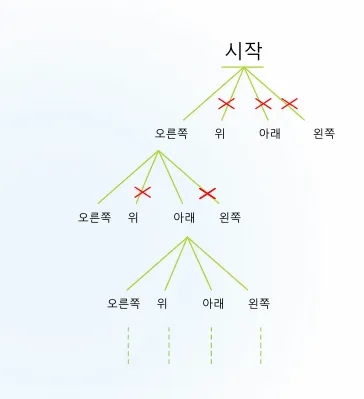
길찾기도 좌우 상하 네개의 경우의 수를 모두 DFS탐색하고 보면된다.
DFS 미로찾기 구현
void dfs(int level, int nowX, int nowY)
C++
복사
만약에 원하는 위치에 도착했다면 "도착"을 출력해보자.
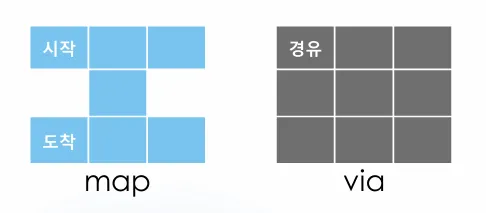
길찾기도 그래프 탐색과 마찬가지로 이미 방문했던곳을 재귀호출해야 한다.
실제 구현 코드
#include <iostream>
int map[3][3] =
{
0, 0, 0,
1, 0, 1,
0, 0, 0,
};
int visited[3][3] =
{
};
void findPathByDFS(int level, int x, int y)
{
if (x == 2 && y == 2)
{
std::cout << "도착";
return;
}
const int direct[4][2] =
{
{0, 1},
{1, 0},
{0, -1},
{-1, 0}
};
for (int i = 0; i < 4; i++)
{
int dx = x + direct[i][0];
int dy = y + direct[i][1];
// 맵을 넘어가는 경우
if (dx < 0 || dx >= 3 || dy < 0 || dy >= 3)
continue;
// 벽에 부딪히는 경우, 방문한 경우
if (map[dy][dx] == 0 && visited[dy][dx] == 0)
{
visited[dy][dx] = 1;
findPathByDFS(level + 1, dx, dy);
visited[dy][dx] = 0;
}
}
}
int main()
{
visited[0][0] = 1;
findPathByDFS(0, 0, 0);
return 0;
}
C++
복사
순열 vs 조합
순열 (Permutation)
순열: 순서에 상관있게 선택해서 나열 하는 것
1, 2, 3 등을 뽑아서 만드는 경우의수 (순서가 중요한 것들)
조합 (Combination)
조합: 많은 것들에 여러개를 뽑아 모아서 만드는 짝
로또번호 (순서는 중요하지 않은 것)
여러명중의 참가자 선택하기
위문제들은 거의 DFS 알고리즘을 이용해서 푸느데 트리 그리는 방식이 다르다.
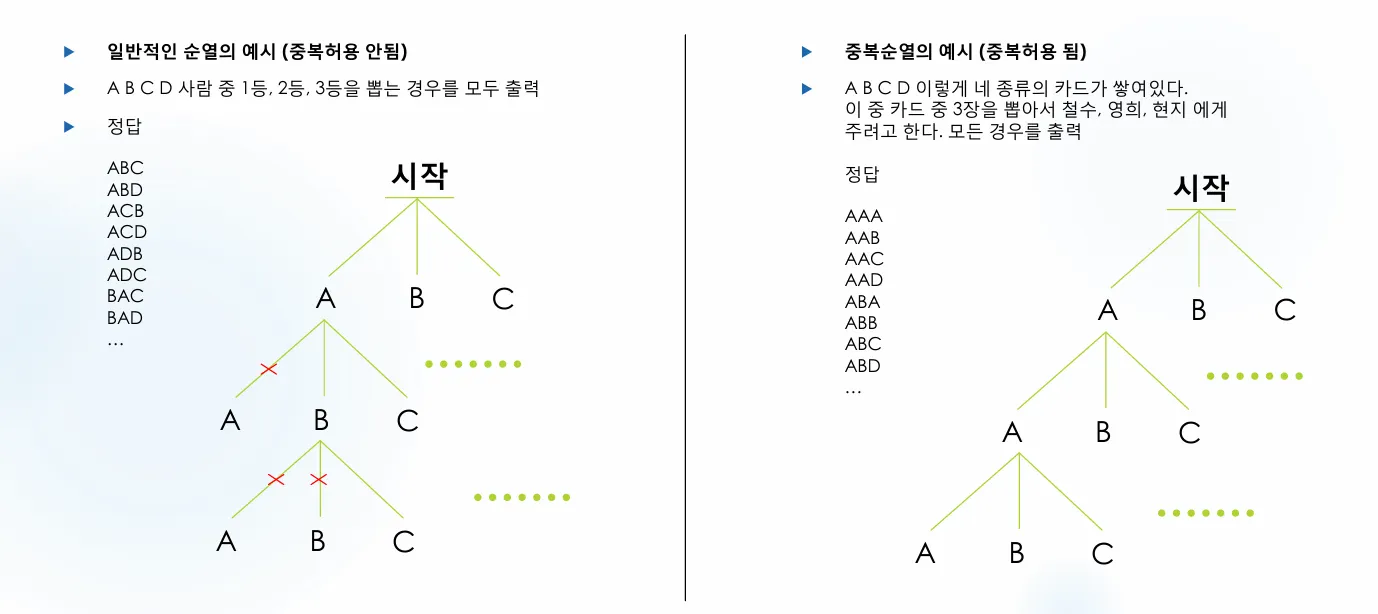
순열 예시
•
일반적인 순열의 예시 (중복허용 안함)
◦
A B C D 형태의 모든 순열을 출력
◦
이 중 카드 중 선정 본 가지가 발견되다
조합 예시
•
중복순열의 예시 (중복허용 함)
◦
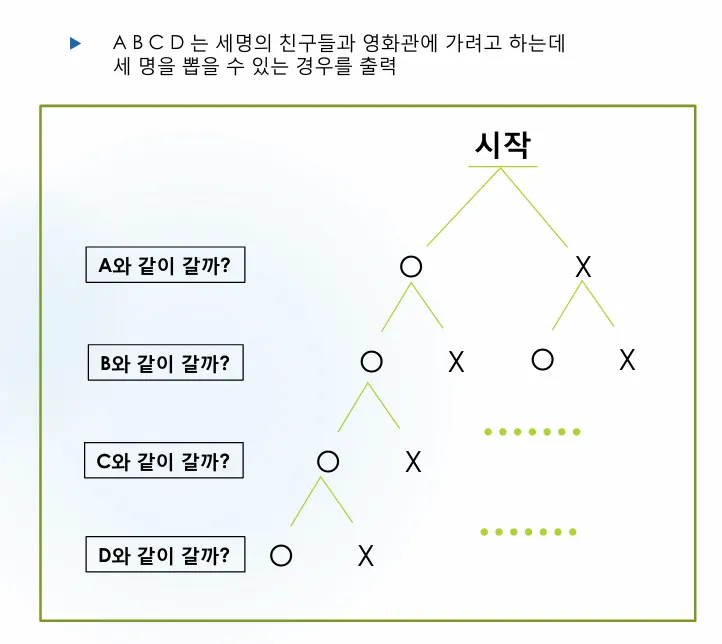
A B C D 는 서로의 친구들과 영화관에 가려고 하는데
◦
세 명을 뽑을 수 있는 경우의 출력
조합 구현 (DFS 활용)
#include <iostream>
char history[10] = {};
char ox[2] = { 'O', 'X' };
char data[10] = "ABCD";
void dfs(int level)
{
int cnt = 0;
if (level == 4)
{
//std::cout << history << std::endl;
for (size_t i = 0; i < 4; i++)
{
if (history[i] == 'O')
{
cnt++;
}
}
if (cnt == 3)
{
for (size_t i = 0; i < 2; i++)
{
if (history[i] == 'O')
{
std::cout << data[i];
}
}
std::cout << std::endl;
}
return;
}
for (size_t i = 0; i < 2; i++)
{
history[level] = ox[i];
dfs(level + 1);
history[level] = 0;
}
}
int main()
{
dfs(0);
}
// Brute-Force, Backtracking, DFS는 비슷한 의미로 인해 혼용에서 쓰이고 갑니다.
// 명확한 용어의 의미는 다음과 같습니다.
// • 완전탐색(Brute-Force): 모든 경우를 시도해보고 답을 찾아내는 방법일 뿐함. 단순 for문 들리는 방법도 있고, 재귀호출을 쓰는 방법도 있음.
// • Backtracking: 많은 경우를 시도하다가 정답이 될 가능성이 없으면 시도을 취소하고, 뒤로 돌아가 다른 시도을 해보는 알고리즘.
C++
복사
주요 개념 정리
트리 순회 방법
•
전위 순회: 루트 → 왼쪽 → 오른쪽
•
중위 순회: 왼쪽 → 루트 → 오른쪽
•
후위 순회: 왼쪽 → 오른쪽 → 루트
미로찾기 핵심
•
4방향 탐색: 상하좌우 이동
•
visited 배열: 중복 방문 방지
•
백트래킹: 탐색 후 원상복구
•
경계 검사: 맵 범위 넘어가지 않도록
순열과 조합
•
순열: 순서가 중요 (A,B,C vs B,A,C 다름)
•
조합: 순서가 무관 (A,B,C vs B,A,C 같음)
•
구현: 모두 DFS + 백트래킹으로 해결
알고리즘 용어
•
완전탐색(Brute-Force): 모든 경우의 수 탐색
•
백트래킹(Backtracking): 조건에 맞지 않으면 되돌아가기
•
DFS: 깊이 우선 탐색으로 구현
이 모든 기법들은 재귀함수와 백트래킹을 기본으로 하며, 문제 상황에 따라 적절히 응용하여 사용합니다.
“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.
자세한 안내 보기: 프리미엄 코칭 안내 바로가기 또는 카카오톡 상담방: 얌얌코딩 상담방