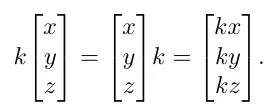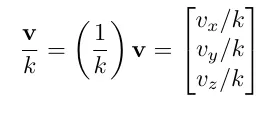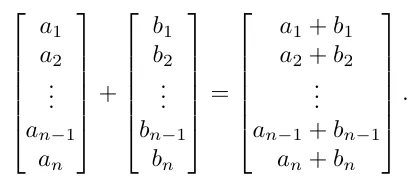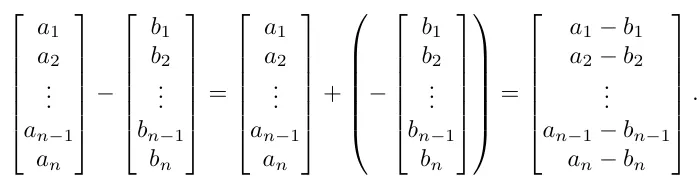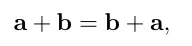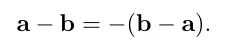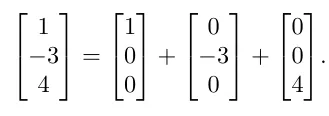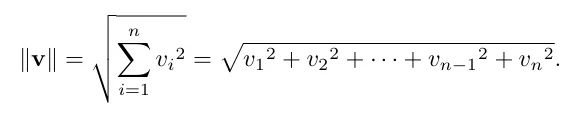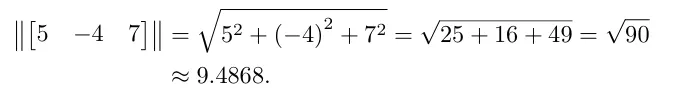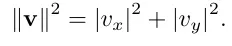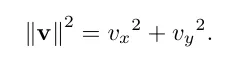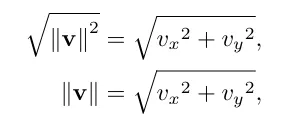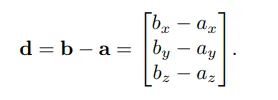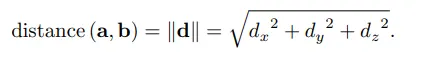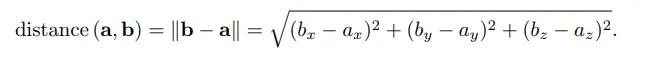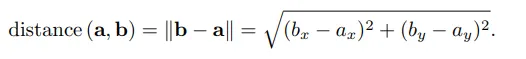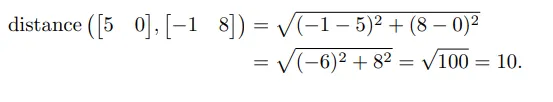Vector Multiplication by a Scalar(벡터의 스칼라 곱셈)
벡터와 스칼라는 기본적으로 더할수 없습니다. 하지만 벡터와 스칼라를 곱할순 있습니다.
벡터와 스칼라 곱셈을 통해서 벡터의 길이, 방향을 바꿀수 있습니다.
벡터와 스칼라의 곱셈은 간단합니다.
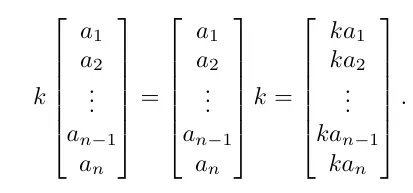
각 벡터의 요소에 스칼라값을 곱해주면 됩니다.
3D 벡터라면 다음과 같은 곱연산이 이루어질것 입니다.
그리고 스칼라와 벡터의 순서는 상관없으나 대부분 스칼라K값을 앞부분에 명시합니다.
또한 벡터는 스칼라값으로 나누어질수도 있습니다.
다양한 벡터들의 스칼라 곱셈을 2D벡터로 표현하면 다음과 같은 그림으로 표현됩니다.
다음은 벡터를 스칼라로 곱할 때 주의해야할 몇가지 점들이 있습니다.
•
벡터와 스칼라를 곱할 때 우리는 일반적인 곱셈기호 X를 쓰지 않습니다. 벡터와 스칼라배 곱셈은 두수를 나란히 나열하는 방법으로 사용합니다. (일반적으로 오른쪽에 벡터를 둔다)
•
벡터의 스칼라 곱셈,나눗셈은 모두 덧셈과 뻴셈 전에 먼저 발생합니다.
•
스칼라는 벡터로 나눌수 없으며 벡터는 다른 벡터로 나눌 수 없습니다.
•
벡터의 음수화는 벡터에 스칼라 -1을 곱하는 연산으로도 볼 수 있습니다.
Vector Addition and subtracion(벡터의 덧셈과 뺄셈)
우리는 두개의 벡터를 더하고 뺄수 있습니다. 단 해당 연산은 동일한 공간(2D,3D)에서 사용가능합니다. 덧셈과 뺼셈을 하는 방법은 동일한 연산 방법을 사용합니다.
두벡터를 더하는 방법은 간단합니다. 각 벡터의 해당 구성요소를 각각 더해주면 됩니다.
백터의 뺄셈도 간단합니다. 각벡터의 해당 구성요소를 순서에 맞추어 뺴주면 됩니다.
3차원 벡터로 예를 들어 봅시다.
벡터는 스칼라로 더하거나 뺄수 없습니다. 또한 다른차원의 벡터와의 연산을 진행 할 수 없습니다.
벡터의 덧셈은 어느 순서인지 간에 같은 벡터가 나옵니다.
벡터의 뺼셈은 순서에 따라서 방향이 달라지는 벡터가 나옵니다.
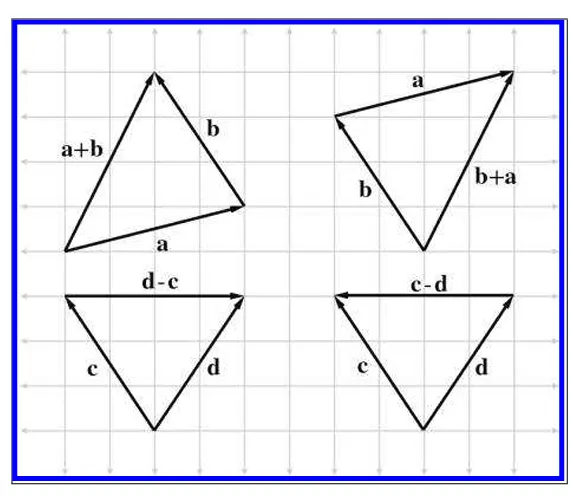
아래는 벡터의 덧셈과 뺼셈을 데카르트 좌표계에서 사용한 예시입니다.
위 그림을 보면 백터의 덧셈은 a→b 또는 b→a 든 순서에 상관없이 결과가 같은 벡터를 나타내지만
뺄셈에서는 c→d, d→c 를 비교하면 반대방향의 벡터가 생성되는걸 볼수 있습니다.
d-c 는 c→d로 이동하는 벡터를 그립니다. c-d는 d→c로 이동하는 벡터를 그립니다.
벡터의 덧셈뺄셈은 그림과 같이 삼각형을 이룹니다.
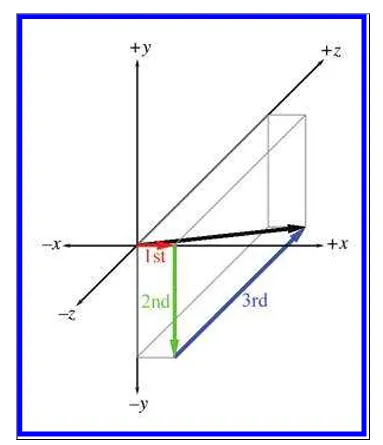
예시로 [1, -3, 4] 벡터가 아래 그림에서 이동한걸 덧셈과 뺼셈 수식으로 표현하면 다음과 같습니다.
Displacement Vector from One point to another(한점에서 다른 점으로의 이동을 표현 하는 벡터)
통상적으로 이것은 우리가 한점에서 다른점으로의 이동을 표현 할때 사용하는 계산 방법입니다.
우리는 벡터의 뺼셈을 이용하여 표현할 것입니다.
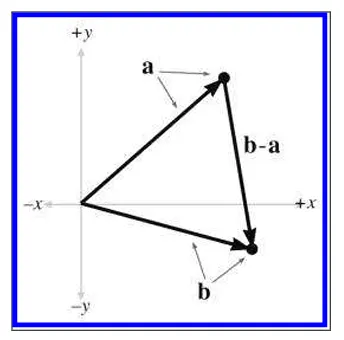
다음 그림은 b-a가 어떻게 a→b의 벡터로 계산 되는지 방법을 보여줍니다.
그림을 보면 a벡터와 b벡터를 원점에서 시작시킵니다. 그리고 삼각형을 그려봅니다.
벡터의 뺄셈 b-a 는 a에서 b까지의 벡터를 표현합니다. 반대로 a-b 는 b에서의 a까지의 벡터를 표현합니다. b-a벡터와 반대되는 벡터입니다. 항상 벡터의 뺄셈은 한벡터에서 다른벡터로의 이동을 표현하는 벡터를 만든다고 이해하면 됩니다.
Vector Manitude(Length) 벡터의 길이
벡터는 크기와 방향을 가지고 있다고 이야기 했습니다. 위 그림들을 보다보면
하지만 크기나 방향을 명시적으로 값을 활용해 표현하고 있지 않다는것을 알수 있습니다.
예를 들어 [3,4] 의 크기는 5입니다. 벡터를 표현할때 따로 크기를 표현하지 않기 떄문에 우리는 크기가 필요할떄는 이를 계산해줘야 합니다.
아래식은 차원에 따른 벡터의 길이를 계산 하는 방법입니다.
벡터의 크기는 벡터 구성 요소의 제곱의 합들의 제곱근입니다. 2D와 3D에서는 더욱 간단하게 표현 가능합니다.
예를 들어 3D 벡터를 예시로 값을 구해봅시다.
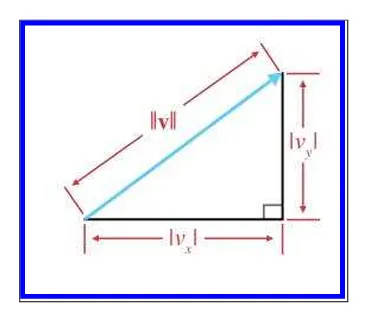
위 방정식이 작동하는 이유를 그림을 그려서 표현해봅시다. 2D 벡터에 한해서 벡터 ||V||는 빗변으로 사용해서 다음과 같은 직각삼각형으로 표현 할 수 있습니다.
피타고라스의 정리에 따르면 직각삼각형의 경우 빗변 길이의 제곱은 다은 두 변의 길이의 제곱의 합과 같습니다.
x,y의 값에 제곱을 하면 양수가 되기 때문에 절대값 기호를 생략 할수 있습니다.
양변에 제곱근을 취하고 단순화 하면 다음과 같은 식이 나옵니다.
물론 3D에서는 조금더 복잡합니다. 하지만 기본적인 원리는 같습니다.
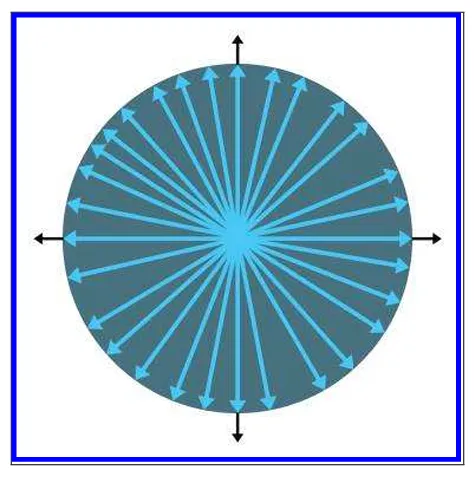
크기가 같은 벡터를 나열 하면 무한하게 존재합니다. 이 벡터들은 모두 길이는 같지만 방향이 다르기 떄문에 그림과 같이 꼬리가 원점에 놓일때 원을 형성합니다.
Unit Vector(단위 벡터)
우리가 앞에서 계속 벡터에 대해서 이야기하면서 느낀 거지만 대부분은 벡터의 길이가 중요한게 아니라 방향만이 중요 했습니다. 단위 벡터는 방향정보만 남긴채 크기가 1인 벡터를 이야기 합니다.
또다른 말로는 normalized(정규화) 벡터 라고도 부릅니다.
떄로는 유닛벡터는 노말이라고도 불립니다. 그러나 용어에 대한 명확한 구분이 필요합니다. 노말은 수직이라는 의미도 내포하고 있기 떄문에 두 용어는 분리해서 사용되어야 합니다.
정규화된(normalized)된 벡터는 항상 단위길이가 1이지만 노말(normal)벡터는 길이가 1인경우도 있지만 아주 간혹 그렇지 않은 경우도 있습니다.
일반적인 벡터를 단위벡터로 만드는 방법은 간단합니다.
각벡터의 요소를 벡터의 길이로 나누어주면 됩니다. 물론 해당 벡터는 0벡터가 아니여야 합니다.
예를들어 2D 벡터 [12, 5]를 유닛벡터로 만들면 다음과 같이 계산됩니다.
당연한 이야기지만 0벡터는 정규화가 불가능 합니다.
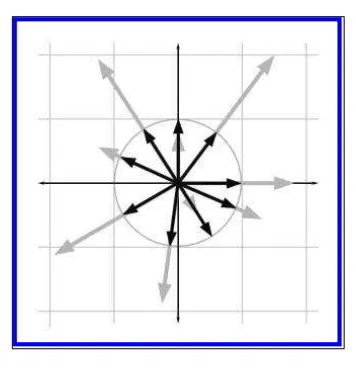
위 그림을 보면 1보다 큰 벡터를 단위벡터로 변경하면 길이가 더 짧아지고
반대로 1보다 작은벡터를 단위벡터로 만들면 길이가 길어집니다.
자 이제 기하학에서의 거리를 구하는 공식을 계산해봅시다.
먼저 거리를 두 점 사이의 선분 길이로 정의 하겠습니다.
벡터는 방향을 가르키는 선분입니다. 그말 인 즉슨 두 점 사이의 거리는 한점에서 다른 점까지의 벡터 길이와 같습니다.
3차원에서 거리공식을 만들어 봅시다. 첫번째로 a에서 b까지의 벡터 d를 계산합니다.
a와 b의 거리는 벡터 d의 길이와 같습니다.
d를 a.b값을 이용해 대체하면 다음과 같습니다.
2차원에서는 더 간단합니다.
예제 :