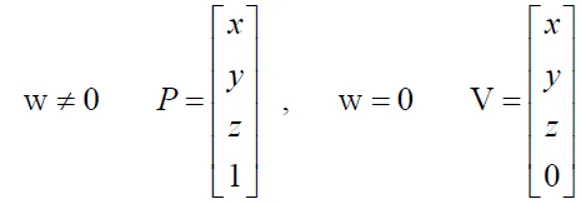숙제
각 구성된 씬에 여러분 게임 제작에 필요햔 배경이미지를 띄어보세요.
데카르트 좌표계는 그림과 같이 수평으로 배치한 첫 번째 실수 집합의 미지수를 x, 수직으로
배치한 두번째 실수 집합의 미지수를 y로 표기하고 원점을 기준으로 x축의 오른편, y축의 위편은
양의 영역을 나타낸다. 이렇게 배치된 두 실수 집합으로 평면을 가르면 평면의 영역은 총 4개의
분면으로 나뉘는데, 오른쪽 상단에서부터 반시계 방향으로 그림과 같이 이름을 붙힌다.
데카르트 좌표계는 한 원소의 곱집합과 동일하게 순서쌍으로 표현하며 좌표(coordinate)라고 부른다.
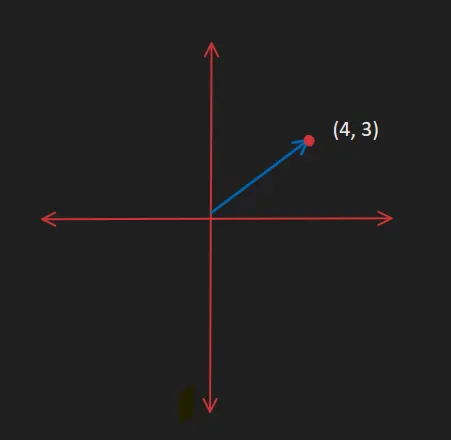
일반적으로 좌표는 수와 동일하게 그림과 같이 점 또는 원점으로부터의 화살표로 표현한
다. 좌표 역시 크기와 방향 두 가지 속성을 지니게 된다.
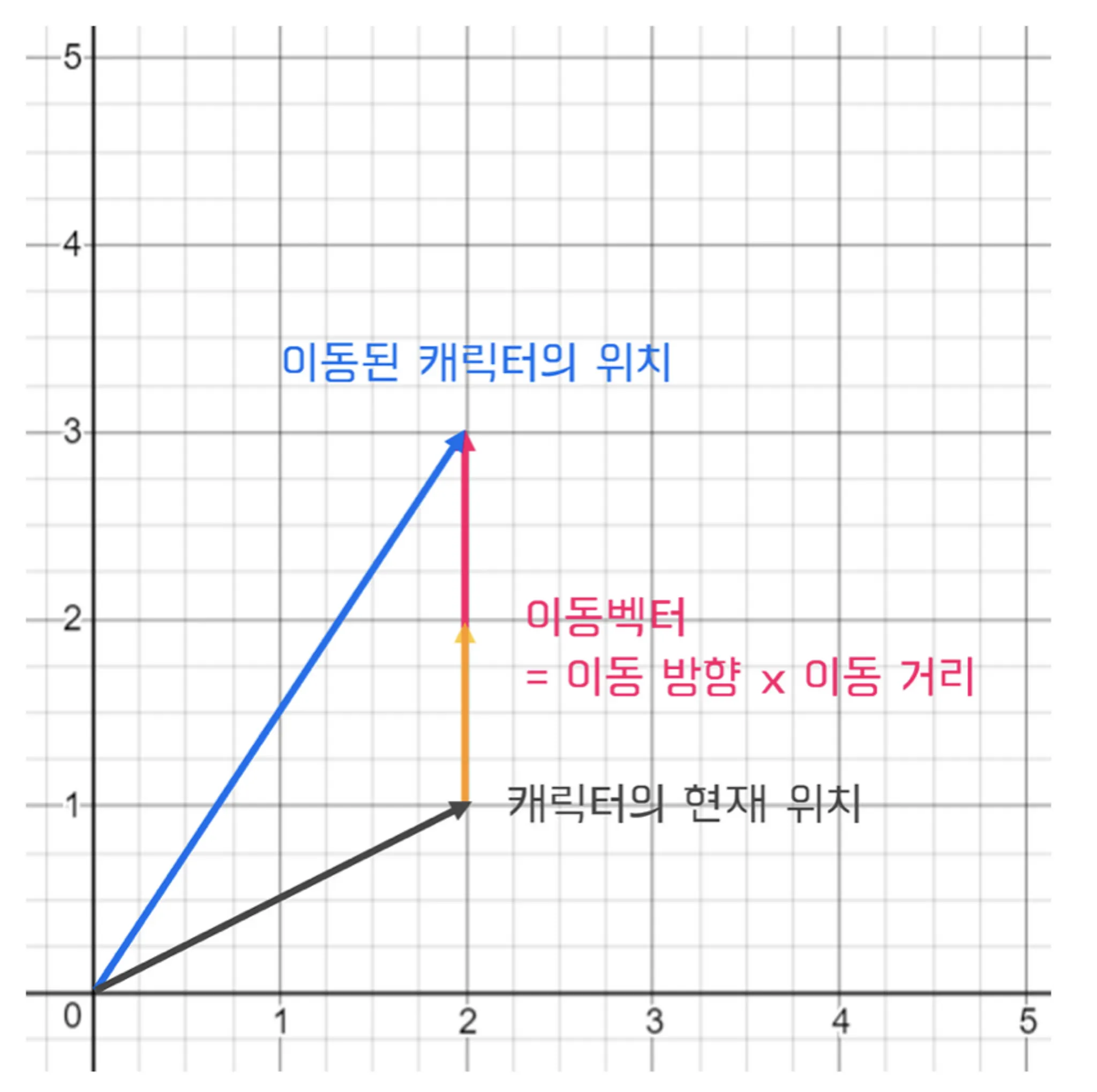
좌표를 다루는 작업은 직선에서 평면으로 무대만 넓어졌을 뿐, 수직선에서 수를 다루는 방식과매우 유사하다. 하지만 평면에서 점이 움직이는 것처럼 보이게 하려면 평면에서 이뤄지는 새로운 연산을 고안해야 할 것이다.
스칼라와 벡터
평면의 좌표 (x, y)는 두 실수 x와 y를 결합해 만들어 진다. 그렇기 떄문에 좌표의 연산은 실수가지니는 연산의 성질을바탕으로 설계돼야 한다.
선형대수학에서 벡터 공간 또는 선형 공간은 원소를 서로 더하거나 주어진 배수로 늘이거나 줄일 수 있는 공간이다. 체(대수학)에 대한, 가군의 특수한 경우다. 벡터 공간의 원소를 벡터라고 하며, 이는 직관적으로 방향 및 길이의 비가 정의된 대상을
나타낸다.
1.
스칼라
크기만 있고 방향이 없는 물리량, 즉 방향성을 가지지 않는 성분이다.
시간, 부피, 질량, 온도, 속력, 에너지, 전위 등
1.
벡터
크기와 방향이있는 물리량, 즉 크기에 방향성을 함께 고려하여야 설명이 가능한 물리량이다.
변위, 속도, 가속도, 힘, 운동량, 충격량, 중력장, 전기장, 자기장 등
•
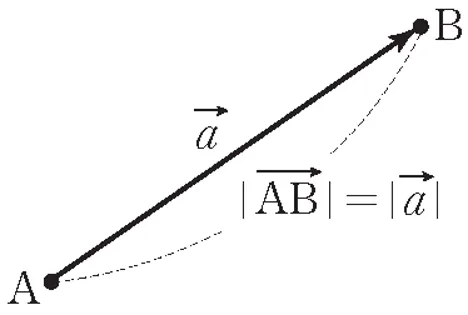
일반적인 벡터
위치 벡터와 벡터
•
그래픽스 수학
P,Q,R : 포인트(point 위치)
u,v,w : 벡터
a,b,y : 스칼라
a : 벡터를 행렬로 표기할 경우
M : 행렬
•
포인트
위치만 표현
예 ) 철수와 영희의 위치
•
벡터 방향과 크기 표현
예 ) 속도, 힘
•
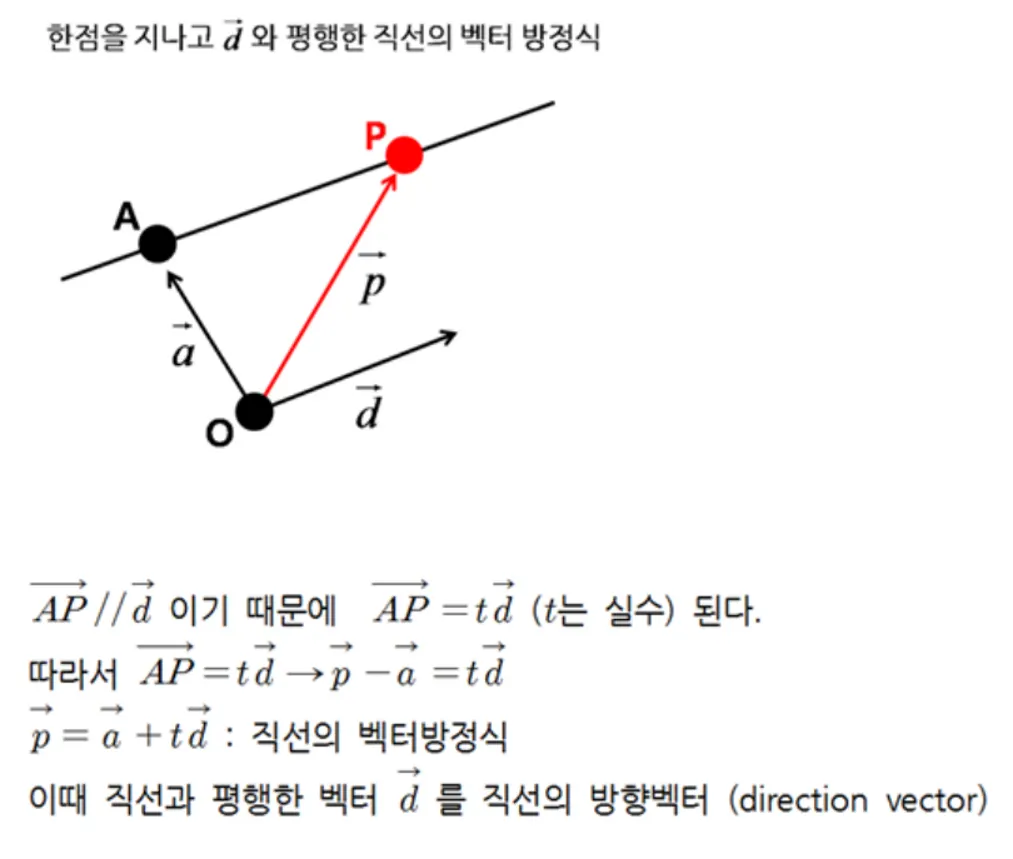
직선( 무한이 긴 선 )의 벡터 방정식
•
벡터 선분( 시작과 끝이 있는 직선 ) 의 방정식
•
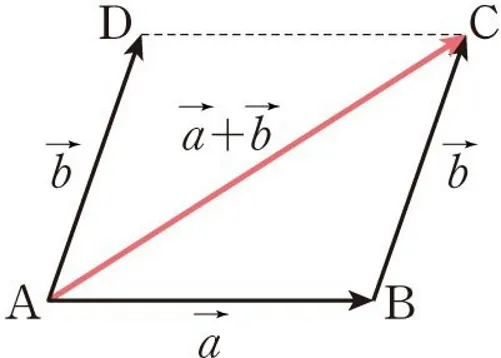
벡터의 덧셈
•
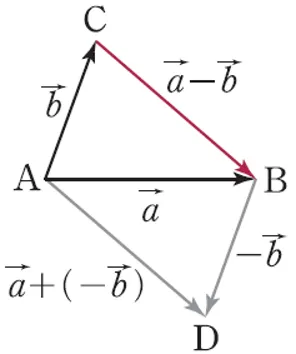
벡터의 뺄셈
•
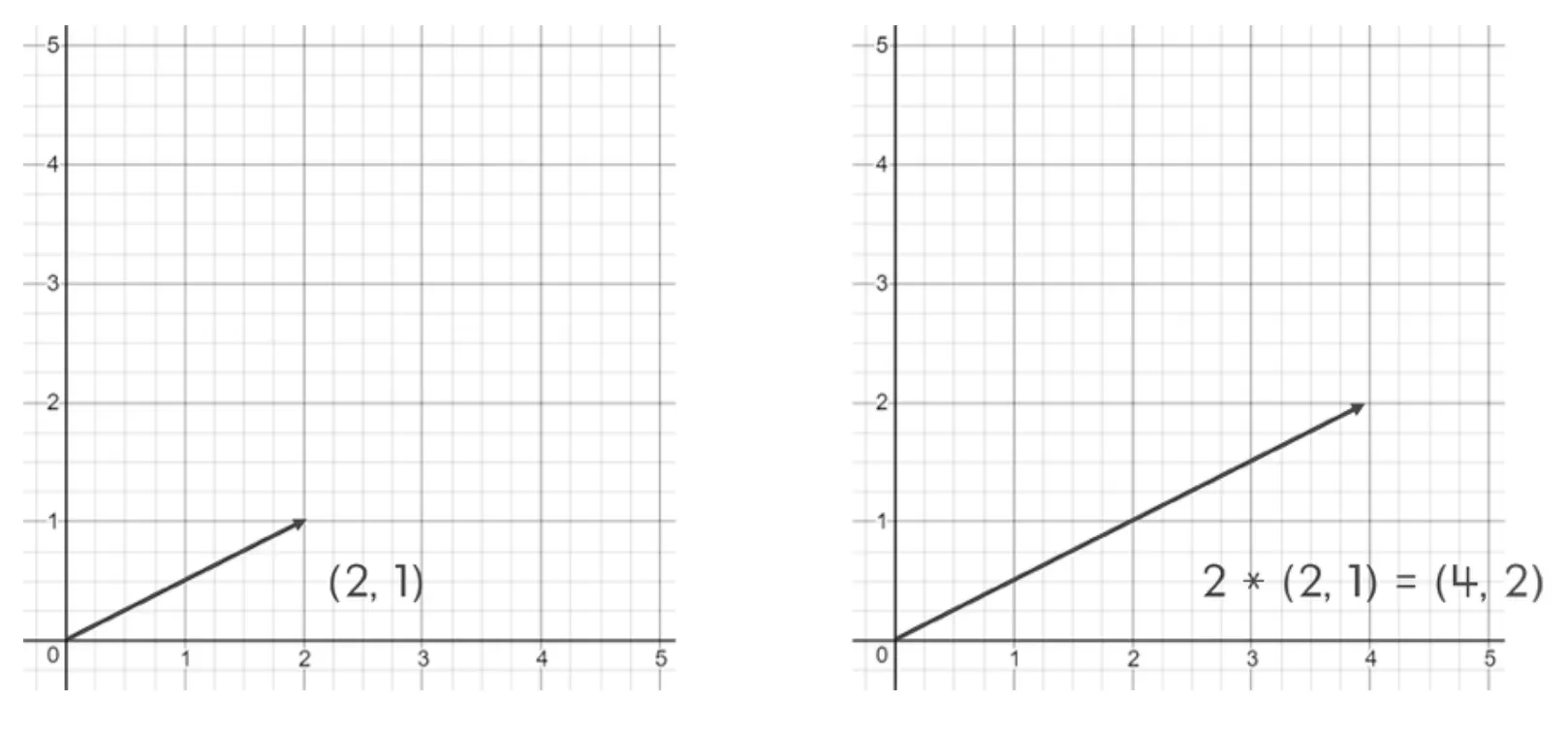
벡터의 곱셈
•
동촤좌표계 ( Homogeneous Coordinates )
[보충] 포인트와 위치 벡터의 구분
•
(지구의 움직임을 고려하지 않는다면) 남산 타워의 위치는 고정되어 있습니다. 보는 사람과 상관 없이 남산 타워의 위치는 동일해야 합니다. 그러나 실제로는 보는 사람의 위치와 방향에 따라서 상대적으로 다르게 보입니다. 예를 들어서 산 밑에서 보는 사람은 올려다 봐야할거고 비행기를 타고 있다면 내려다 봐야겠지요.
•
포인트는 보는 사람과 상관 없는 남산 타워의 고유의 성질로써의 위치를 다룰 때 사용하는 개념이고 위치 벡터는 특정 좌표계를 기준으로 남산 타워의 위치를 정의할 때 사용하는 도구입니다.
•
동일한 포인트가 좌표계에 따라서 서로 다른 위치 벡터로 표현이 됩니다. 온도에 비유하자면 물의 끓는 온도는 물 고유의 성질이지만 그 온도를 숫자로 표현을 하면 화씨 표현법(212F)과 섭씨 표현법(100C)에서 각기 서로 다른 숫자로 표현이 됩니다.
•
벡터 만으로는 위치를 표현할 수 없습니다. 벡터로 위치를 표현하기 위해서는 기준점과 기준 방향이 필요합니다. 그래서 어떤 좌표축의 원점과 좌표축 방향을 기준으로 위치를 표현하는 것을 위치 벡터라고 구분해서 부르는 것입니다.
[보충] Affine
•
일반 영어에서 "Affine"이란 단어를 사용하는 것은 본 적이 없어서 일반적인 의미는 잘 모르겠습니다. 발음은 사전에서 찾아보면 "어파인" 인데 유튜브의 그래픽스 강의들을 찾아보면 모두 "애파인"이라고 발음합니다.
•
그래픽스와 관련된 기하학에서 "Affine"은 Affine transformation에서 사용하는 단어인데 점, 직선, 평면을 변환했을 때 계속 점, 직선, 평면으로 유지되는 것을 의미합니다. 예를 들어서 3차원 공간의 직선에 애파인 변환을 적용하면 (곡선이 되지 않고) 직선이 됩니다. 참고로 직선이 점(길이가 0인 직선)으로 변환될 수도 있습니다. 광추적에서 배운 내용을 기준으로 예를 들자면 3차원 공간의 평면을 렌더할 때 2차원 공간으로 투영 되는 변환이 애파인 변환입니다. 레스터화에서 어떻게 처리하는 지는 뒤에 나옵니다.
•
보통 애파인 변환을 선형 변환(Linear transformation)과 비교합니다. 선형 변환에 이동을 추가한 것이 애파인 변환입니다. 벡터에는 절대적인 위치 개념이 없기 때문에 이동을 정의하기 위해서는 포인트가 필요합니다. 그래서 포인트들 끼리의 weighted average에 Affine combination이란 이름이 붙은 것입니다. 다만, 왜 가중치의 합이 1인 경우만 affine combination이라고 부르는 지에 대해서는 저도 확인을 해보지 않았습니다.