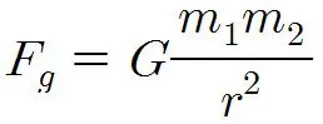이제 간단한 물리 시스템도추가해보자.
리지드 바디 컴포넌트를 설계하고 추가 해도록 하겠다.
다양한 기능은 들어가지않고 간단한 이동과 중력정도만 힘을 붙여주는 방식으로 추가된다.
void Rigidbody::Update()
{
// f(힘) = m(질량) x a(가속도)
// a = f / m;
mAccelation = mForce / mMass;
// 속도에 가속도를 더한다.
mVelocity += mAccelation * Time::DeltaTime();
if (mbGround)
{
// 땅위에 있을때
Vector2 gravity = mGravity;
gravity.normalize();
float dot = Vector2::Dot(mVelocity, gravity);
mVelocity -= gravity * dot;
}
else
{
// 공중에 있을떄
mVelocity += mGravity * Time::DeltaTime();
}
//최대 속도 제한
Vector2 gravity = mGravity;
gravity.normalize();
float dot = Vector2::Dot(mVelocity, gravity);
gravity = gravity * dot;
//좌우 속도만 추출
Vector2 sideVelocity = mVelocity - gravity;
//최대중력가속도보다 크다면 최대 중력가속도로 전
if (mLimitedVelocity.y < gravity.length())
{
gravity.normalize();
gravity *= mLimitedVelocity.y;
}
// 최대속도보다 크다면 최대속도로 변환
if (mLimitedVelocity.x < sideVelocity.length())
{
sideVelocity.normalize();
sideVelocity *= mLimitedVelocity.x;
}
mVelocity = gravity + sideVelocity;
// 적용된 힘이 없고 속도가 0이 아닐 떄(마찰력의 조건)
if (!(mVelocity == Vector2::Zero))
{
//속도에 반대방향으로 마찰력 작용
Vector2 friction = -mVelocity;
friction = friction.normalize() * mFriction * mMass * Time::DeltaTime();
// 마찰력으로 인한 속도 감소량이 현재 속도보다 큰 경우
if (mVelocity.length() <= friction.length())
{
// 멈춰
mVelocity = Vector2::Zero;
}
else
{
// 속도에서 마찰력으로 인한 반대방향으로 속도를 차감
mVelocity += friction;
}
}
//계산된 속도에 맞게 위치를 조정
Transform* tr = GetOwner()->GetComponent<Transform>();
Vector2 pos = tr->GetPosition();
pos = pos + mVelocity * Time::DeltaTime();
tr->SetPosition(pos);
mForce.clear();
}
C++
복사
중력: 가장 기본적인 현실의 작동원리
현실에 존재하는, 또는 적어도 현실의 구조를 떠올릴 수 있는 정도의 논리 구조를 갖추어야 플레이어들에게 수용될 수 있는 것이 게임의 논리 구조다.
그리고 그 현실의 영역에서 가장 광범위한 영향력을 가지고 있는 구조라면 역시 중력일 것이다. 우리가 사는 세계(단지 인류의 세계인 지구라는 범주를 넘어서 범우주급으로 그 의미를 넓힌다 하더라도)는 중력에 의해 존재하는 세계다. 무한대에 달하는 중력의 영향 범위하에서 살고 있기에
우리는 지구가 둥글다는 사실을 알아도 둥근 표면에 발을 붙이고 산다는 것을 그리 이상하게 여기지 않는다. 이처럼 광범위한 영향력을 지닌 중력이기에 많은 게임 또한 중력에 대한 표현이 현실감의 재현을 위해 매우 중요한 논리 구조로 자리한다.
때문에 많은 게임이 직간접적으로 중력에 대한 표현을 포함한다. '슈퍼 마리오'의 점프 동작이 자연스러워 보이는 것은 그 점프를 구현하는 데 중력가속도에 의한 움직임이 포함되기 때문이다. 단지 점프 키를 눌렀을 때 세로로만 올라갔다 내려오는 것으로는 점프라는 느낌을 주기 힘들다.
초창기 게임에서도 점프 동작 하나에 중력가속도를 고려했을 정도였는데, 기술에 의해 표현력이 비약적으로 상승한 오늘날의 게임들에는 아예 물리 엔진이라는 이름으로 중력가속도와 물체의 운동을 표현하는 기본 세팅들이 포함되어 탑재됨으로써 비로소 세계의 현실적 구현을 완성하곤 한다.
F g 는 각 입자에 작용하는 힘의 크기이고, m 1 , m 2 는 각각 물체의 질량, r은 두 물체 사이의 거리, G는 중력상수이다. 이것은 '질량이 있는 모든 물체는 다른 물체를 끌어당기며, 그 힘은 물체들의 질량의 곱에 비례하고 그 사이의 거리의 제곱에 반비례 한다.'를 의미한다.
if (mbGround)
{
// 땅위에 있을때
Vector2 gravity = mGravity;
gravity.normalize();
//물리에서의 내적은 두 벡터의 작용 효율성 나타낸다.
//내적의 값이 해당 방향으로 얼마만큼의 효율을 계산하기 떄문에
//실제 중력은 밑으로만 작용하지만 게임에서는 빗면에서는 중력이 대각으로 작용할수
//있기 떄문에 내적을 이용해서 계산해주었다.
float dot = Vector2::Dot(mVelocity, gravity);
mVelocity -= gravity * dot;
}
else
{
// 공중에 있을떄
mVelocity += mGravity * Time::DeltaTime();
}
C++
복사