순열 알고리즘 수업노트
기본 개념
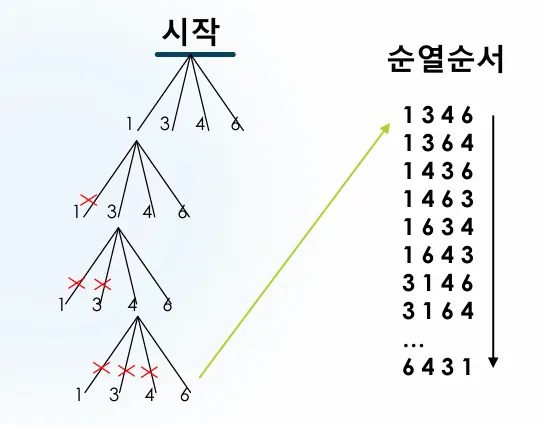
내장의 카드를 모두 이용하여 순차를 출력하고자 한다.
카드 예시
[1] [3] [4] [6]
Plain Text
복사
중복을 허용하지 않는 순열을 처리하는 방법
트리 구조로 순열 생성 과정:
순열순서:
•
1346, 1364, 1436, 1463, 1634, 1643
•
3146, 3164, ...
•
6431
순열 알고리즘 규칙 1
재귀호출을 돌리지 않고, 다음과 같은 규칙으로 구할 수 있다.
1.
맨 오른쪽 부터 숫자부터 2개씩 비교한다.
2.
왼쪽보다 오른쪽 숫자가 더 큰 index를 찾아서 빨간색으로 체크한다.
3.
예를 들어서 1 6 5 3 이라면 1 6 5 3 (1단계)
4.
예를 들어서 5 6 17 이라면 5 6 1 7 (1단계)
5.
예를 들어서 7 8 1 1 이라면 7 8 1 1 (1단계)
이렇게 찾은 index를 a라고 하자.
순열 알고리즘 규칙 2
1.
다시 맨 오른 쪽 숫자부터 a까지 숫자를 찾자.
2.
[a]보다 더 큰 숫자를 발견하면 파란색으로 표시하자
3.
빨간색과 파란색 index값을 찾아내서 swap해주자
4.
예를 들어서 1 6 5 3 이라면 1 6 5 3 : 3 6 5 1 (2단계)
5.
예를 들어서 5 6 17 이라면 5 6 1 7 : 5 6 7 1 (2단계)
6.
예를 들어서 7 8 1 1 이라면 7 8 1 1 : 8 7 1 1 (2단계)
순열 알고리즘 규칙3
1.
a index 다음 숫자부터 맨 끝까지 숫자를 전부 뒤집음 (swap)
2.
만약에 a뒤에 숫자가 3개있으면 3개다 뒤집음
3.
예를 들어서 1 6 5 3 이라면 1 6 5 3 → 3 6 5 1 → 3 1 5 6 (3단계)
4.
예를 들어서 5 6 17 이라면 5 6 1 7 → 5 6 7 1 → 5 6 7 1 (3단계)
5.
예를 들어서 7 8 1 1 이라면 7 8 1 1 → 8 7 1 1 → 8 1 1 7 (3단계)
DFS를 이용한 순열 생성
재귀함수와 백트래킹 방식
#include <iostream>
char history[5] = "";
char cards[5] = "1234";
int visited[10] = { };
void dfs(int level)
{
if (level == 4)
{
std::cout << history << std::endl;
return;
}
for (int i = 0; i < 4; i++)
{
if (visited[i] == 0)
{
history[level] = cards[i];
visited[i] = 1;
dfs(level + 1);
visited[i] = 0;
history[level] = 0;
}
}
}
C++
복사
DFS 방식의 특징
•
visited 배열: 중복 사용 방지
•
history 배열: 현재까지의 순열 저장
•
백트래킹: 재귀 호출 후 원상복구
•
깊이 우선: 하나의 경로를 끝까지 탐색 후 다음 경로
NextPermutation을 이용한 순열 생성
#include <iostream>
char history[5] = "";
char cards[5] = "1234";
int visited[10] = { };
void dfs(int level)
{
if (level == 4)
{
std::cout << history << std::endl;
return;
}
for (int i = 0; i < 4; i++)
{
if (visited[i] == 0)
{
history[level] = cards[i];
visited[i] = 1;
dfs(level + 1);
visited[i] = 0;
history[level] = 0;
}
}
}
int nextPermutation(int* data, int n)
{
// 오른쪽 왼쪽으로 a찾기 (index)
int i = n - 1;
while (i > 0 && data[i - 1] >= data[i])
i -= 1;
if (i <= 0)
return 0;
// 오른쪽에서 왼쪽으로 b찾기 (index)
int j = n - 1;
while (data[j] <= data[i - 1])
j -= 1;
// swap data[i-1] and data[j]
int temp = data[i - 1];
data[i - 1] = data[j];
data[j] = temp;
//a값 이후의 위치부터 전부 뒤집기
j = n - 1;
while (i < j)
{
temp = data[i];
data[i] = data[j];
data[j] = temp;
i += 1;
j -= 1;
}
return 1;
}
int main()
{
dfs(0);
std::cout << "===========nextPermutation===========" << std::endl;
int data[4] = { 1,2,3,4 };
int x;
int n = 4;
int result;
while (true)
{
for (x = 0; x< 4; x++)
{
std::cout << data[x];
}
std::cout << std::endl;
result = nextPermutation(data, n);
if (result == 0)
break;
}
return 0;
}
C++
복사
두 방식의 비교
DFS 재귀 방식
장점:
•
구현이 직관적이고 이해하기 쉬움
•
백트래킹 개념 학습에 좋음
•
조건부 순열 생성 용이
단점:
•
재귀 호출로 인한 스택 메모리 사용
•
깊이가 깊어지면 스택 오버플로우 위험
NextPermutation 방식
장점:
•
메모리 사용량 적음 (반복문 사용)
•
사전식 순서로 순열 생성
•
표준 라이브러리 std::next_permutation 사용 가능
단점:
•
알고리즘 이해가 복잡함
•
초기 배열이 오름차순으로 정렬되어야 함
활용 예시
완전탐색(Brute Force) 문제
•
암호 조합: 모든 가능한 비밀번호 생성
•
최적 경로: 모든 경로 조합 탐색
•
조합 최적화: 최적의 배치 찾기
순열의 특성
•
n개 요소의 순열: n! 개
•
4개 카드 순열: 4! = 24개
•
중복 없음: 각 요소는 한 번만 사용
시간 복잡도
•
DFS 방식: O(n × n!)
•
NextPermutation: O(n!) (전체 순열 생성시)
•
공간 복잡도: O(n) (배열 크기)
핵심 포인트
1.
순열: 순서가 중요한 배열 (ABC ≠ BCA)
2.
중복 제거: visited 배열로 중복 사용 방지
3.
백트래킹: 탐색 후 상태 복원
4.
사전식 순서: NextPermutation은 사전순으로 생성
5.
실용성: 완전탐색, 최적화 문제에 활용
순열 알고리즘은 완전탐색과 최적화 문제의 기초가 되는 중요한 알고리즘입니다.
그래프 DFS 수업노트
그래프 DFS 기본 개념
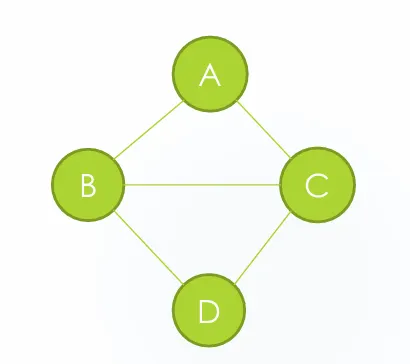
그래프 구조
DFS 그래프 경로찾기
A에서 D로가는 경로 중 네가지 경로가 있다.
가능한 경로들:
•
A-B-D
•
A-B-C-D
•
A-C-D
•
A-C-B-D
기존 TREE DFS와 크게 다르지 않다.
프로토 타입: void dfs(int level, int now)
return 조건이: name[now] == 'D' 라면
그래프니가 사이클생길수 있다. 무한재귀가 발생하지 않도록뭔가를 중복여부를 체크해야한다.
#include <iostream>
char name[5] = "ABCD";
int data[4][4] =
{
0,1,1,0,
1,0,1,1,
1,1,0,1,
0,1,1,0,
};
char history[5] = "";
int count = 0;
int visited[4] = { };
bool IsPossible(int now, int select)
{
if (data[now][select] == 0)
return false;
if (visited[select] == 1)
return false;
return true;
}
void dfs(int level, int now)
{
if (name[now] == 'D')
{
count++;
std::cout << history << std::endl;
return;
}
for (int i = 0; i < 4; i++)
{
if (IsPossible(now, i) == true)
{
visited[i] = 1;
history[level + 1] = name[i];
dfs(level + 1, i);
history[level + 1] = 0;
visited[i] = 0;
}
}
}
int main()
{
history[0] = name[0];
visited[0] = 1;
dfs(0, 0);
return 0;
}
JavaScript
복사
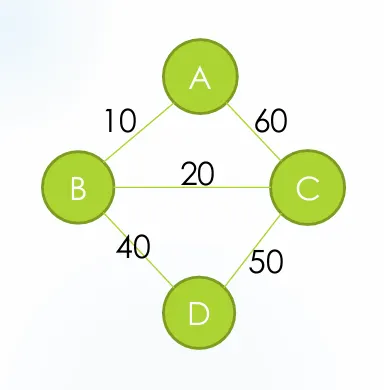
가중치 있는 그래프 탐색
가중치 그래프 구조
A에서 D까지 가는 최소비용 Route찾는다.
인접행렬에서 0과 1대신에 가중치값을 넣어주고전달인자에 sum 변수를 추가하여 누적합을 계산해준다.진입할때 sum을 더하고 다음 시점으로 이동한다.
가중치 그래프 DFS 구현
전체 구현 코드
#include <iostream>
char name[5] = "ABCD";
int data[4][4] =
{
0,10,60,0,
10,0,20,40,
60,20,0,50,
0,40,50,0,
};
char history[5] = "";
int count = 0;
int IsPossible(int level, int select)
{
for (int i = 0; i < level; i++)
{
if (history[i] == name[select])
{
return 0;
}
}
return 1;
}
void dfs(int level, int now, int sum)
{
if (name[now] == 'D')
{
count++;
std::cout << history << std::endl;
return;
}
for (int i = 0; i < 4; i++)
{
if (data[now][i] > 1)
{
if (IsPossible(level, i) == 1)
{
history[level + 1] = name[i];
dfs(level + 1, i, sum + data[now][i]);
history[level + 1] = 0;
}
}
}
}
int main()
{
history[0] = name[0];
dfs(0, 0, 0);
return 0;
}
C++
복사
코드 분석
주요 변수
•
name[5] = "ABCD": 노드 이름 배열
•
data[4][4]: 가중치 인접행렬
•
history[5]: 현재까지의 경로 저장
•
count: 경로 개수 카운터
핵심 함수들
IsPossible 함수
int IsPossible(int level, int select)
{
for (int i = 0; i < level; i++)
{
if (history[i] == name[select])
{
return 0; // 이미 방문한 노드
}
}
return 1; // 방문 가능한 노드
}
C++
복사
기능: 중복 방문 검사 (사이클 방지)
DFS 함수
void dfs(int level, int now, int sum)
{
if (name[now] == 'D') // 목표 도달
{
count++;
std::cout << history << std::endl;
return;
}
for (int i = 0; i < 4; i++)
{
if (data[now][i] > 1) // 연결된 노드 확인
{
if (IsPossible(level, i) == 1) // 방문 가능 확인
{
history[level + 1] = name[i]; // 경로에 추가
dfs(level + 1, i, sum + data[now][i]); // 재귀 호출
history[level + 1] = 0; // 백트래킹
}
}
}
}
C++
복사
알고리즘 동작 과정
1단계: 초기화
•
시작점: A (index 0)
•
history[0] = 'A': 시작점을 경로에 기록
•
sum = 0: 초기 비용
2단계: 탐색 과정
1.
현재 노드에서 연결된 모든 노드 확인
2.
가중치 > 1인 노드만 고려 (data[now][i] > 1)
3.
IsPossible로 중복 방문 검사
4.
조건 만족시 재귀 호출
3단계: 목표 도달
•
name[now] == 'D': 목표 노드 D 도달
•
경로 출력 및 카운트 증가
•
return으로 백트래킹
4단계: 백트래킹
•
history[level + 1] = 0: 경로에서 제거
•
다음 가능한 경로 탐색
가중치 그래프의 특징
인접행렬 표현
int data[4][4] =
{
0,10,60,0, // A: B(10), C(60)
10,0,20,40, // B: A(10), C(20), D(40)
60,20,0,50, // C: A(60), B(20), D(50)
0,40,50,0, // D: B(40), C(50)
};
C++
복사
주요 차이점
•
0: 연결되지 않음
•
양수: 가중치 (비용, 거리 등)
•
대칭 행렬: 무방향 그래프
트리 DFS vs 그래프 DFS 비교
구분 | 트리 DFS | 그래프 DFS |
사이클 | 없음 | 있을 수 있음 |
중복 검사 | 불필요 | 필수 |
백트래킹 | 간단 | 복잡 (경로 복원) |
종료 조건 | 리프 노드 | 목표 노드 |
메모리 사용 | 적음 | 많음 (history 배열) |
실제 활용 사례
1. 최단 경로 문제
•
네비게이션: 도시 간 최단 거리
•
네트워크 라우팅: 최소 비용 경로
•
게임 AI: 캐릭터 이동 경로
2. 경로 탐색
•
미로 찾기: 출구까지의 모든 경로
•
퍼즐 게임: 목표 상태까지의 해법
•
물류 최적화: 배송 경로 탐색
3. 그래프 분석
•
연결성 검사: 노드 간 연결 여부
•
사이클 검출: 순환 구조 발견
•
부분 그래프 탐색: 특정 조건 만족 경로
핵심 포인트
1.
사이클 방지: IsPossible 함수로 중복 방문 검사
2.
백트래킹: 탐색 후 상태 복원
3.
가중치 처리: sum 변수로 비용 누적
4.
경로 추적: history 배열로 경로 기록
5.
조건 검사: data[now][i] > 1로 연결 확인
그래프 DFS는 복잡한 네트워크에서 경로를 찾는 강력한 도구입니다.