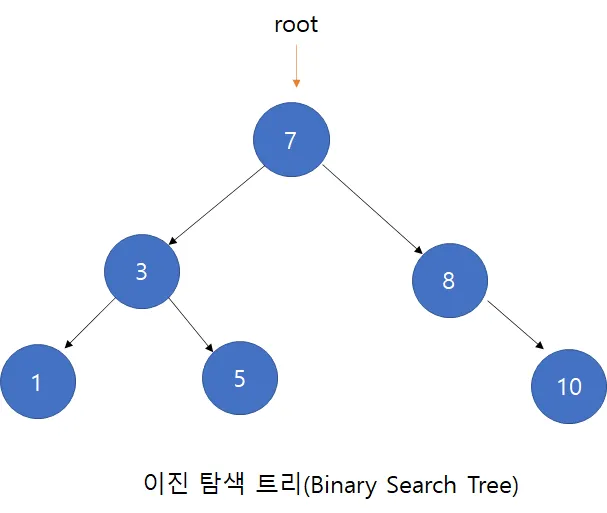
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리란?
•
이진 탐색의 속성이 이진 트리에 적용된 특별한 형태의 이진 트리
이진 탐색이란?
•
이진 탐색 알고리즘이란 정렬된 데이터 중에서 특정한 값을 찾기 위한 탐색 알고리즘 중 하나다.
•
이진 탐색 알고리즘은 오름차순으로 정렬된 정수의 배열을 같은 크기의 두 부분 배열로 나눈 후, 두 부분 중 탐색이 필요한 부분에서만 탐색하도록 탐색 범위를 제한하여 원하는 값을 찾는 알고리즘입니다.
1.
배열의 중간에 내가 찾고자 하는 값이 있는지 확인한다.
2.
중간값이 내가 찾고자 하는 값이 아닐 경우,
•
오름차순으로 정렬된 배열에서 중간값보다 큰 값인지 작은 값인지 판단한다.
3.
찾고자 하는 값이 중간값보다 작은 값일 경우,
•
배열의 맨 앞부터 중간값 전까지의 범위를 탐색 범위로 잡고 탐색을 반복 수행한다.
4.
찾고자 하는 값이 중간값보다 큰 값일 경우,
•
배열의 중간값의 다음 값부터 맨 마지막까지를 탐색 범위로 잡고 탐색을 반복 수행한다.
•
이진 탐색 트리는 이러한 이진 탐색의 알고리즘이 이진 트리에 적용된 형태로 트리의 루트노드는 이진 탐색에서 리스트의 중간값이 된다.
•
루트노드의 왼편 서브 트리의 값들은 이진 탐색 알고리즘에 기반하여 모두 루트노드의 값보다 작은 값들이 자리 잡고 있고 루트노드의 오른편 서브 트리의 값들은 루트노드의 값보다 큰 값들이 자리 잡고 있어야 한다.
◦
Left < root < Right
정리하자면 다음과 같다.
각 노드에 중복되지 않는 키(Key)가 있다.루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.좌우 서브 트리도 모두 이진 탐색 트리여야 한다.
즉 이진 탐색 트리(Binary Search Tree)는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있다.
이진탐색트리 insert(삽입) 코드 - while문 활용
#include <iostream>
#include <vector>
#include <list>
#include <string>
#include <algorithm>
#include <map>
int bst[256] = { 0, };
void insert(int data)
{
int idx = 1;
while (1)
{
if (bst[idx] == 0)
{
bst[idx] = data;
break;
}
else if (bst[idx] > data)
{
idx = idx * 2;
}
else
{
idx = idx * 2 + 1;
}
}
}
int main()
{
insert(10);
insert(5);
insert(15);
//insert(8);
//insert(3);
//insert(7);
//insert(12);
return 0;
}
C++
복사
이진탐색트리 insert(삽입) 코드 - 재귀함수 활용
#include <iostream>
#include <vector>
#include <list>
#include <string>
#include <algorithm>
#include <map>
int bst[256] = { 0, };
void insertRescursive(int data, int now)
{
if (bst[now] == 0)
{
bst[now] = data;
return;
}
if (bst[now] > data)
{
insertRescursive(data, now * 2);
}
else
{
insertRescursive(data, now * 2 + 1);
}
}
int main()
{
insertRescursive(10, 1);
insertRescursive(5, 1);
insertRescursive(15, 1);
insertRescursive(8, 1);
return 0;
}
C++
복사
이진탐색트리 Search(탐색) 코드 - while문, 재귀함수 활
#include <iostream>
#include <vector>
#include <list>
#include <string>
#include <algorithm>
#include <map>
int bst[256] = { 0, };
void insert(int data)
{
int idx = 1;
while (1)
{
if (bst[idx] == 0)
{
bst[idx] = data;
break;
}
else if (bst[idx] > data)
{
idx = idx * 2;
}
else
{
idx = idx * 2 + 1;
}
}
}
void insertRescursive(int data, int now)
{
if (bst[now] == 0)
{
bst[now] = data;
return;
}
if (bst[now] > data)
{
insertRescursive(data, now * 2);
}
else
{
insertRescursive(data, now * 2 + 1);
}
}
void search(int data)
{
int idx = 1;
while (1)
{
if (bst[idx] == 0)
{
printf("Not Found\n");
break;
}
if (bst[idx] == data)
{
printf("Found\n");
break;
}
if (bst[idx] > data)
{
idx = idx * 2;
}
else
{
idx = idx * 2 + 1;
}
}
}
void searchRecursive(int data, int now)
{
if (bst[now] == 0)
{
printf("Not Found\n");
return;
}
if (bst[now] == data)
{
printf("Found\n");
return;
}
if (bst[now] > data)
{
searchRecursive(data, now * 2);
}
else
{
searchRecursive(data, now * 2 + 1);
}
}
int main()
{
// Binary Search Tree
// 데이터를 탐색하는데 있어서 효율성 높다.
// 3가지 동작을 기본으로 둔다.
// 데이터를 저장하는 Insert
// 데이터를 찾는 Search
// 데이터를 삭제하는 Delete
// insert, serach 위조루 보겠다.
// 사용하는 제일 큰 이유는 데이터를 더 빨리 찾기위해 사용하는 자료구조이다.
//insert(10);
//insert(5);
//insert(15);
//insert(8);
//insert(3);
//insert(7);
//insert(12);
insertRescursive(3, 1);
insertRescursive(5, 1);
insertRescursive(1, 1);
insertRescursive(2, 1);
insertRescursive(4, 1);
insertRescursive(7, 1);
return 0;
}
C++
복사
유니온 파인드 알고리즘: 상호 배타적 집합, Disjoin-set(서로소 집합) 이라고도 부른다. 여러 노드가 존재할 때 어떤 두 개의 노드를 같은 집합으로 묶어 주고, 어떤 두 노드가 같은 집합에 있는지 확인하는 알고리즘이다.
왜 이름이 유니온 파인드인가?
유니온 파인드 알고리즘은 두가지의 연산을 진행한다. 이 연산 과정을 Union, Find라고 부른다.
•
Union: 서로 다른 두 개의 집합을 하나의 집합으로 병합하는 연산을 말한다. 이 자료구조에서는 상호 배타적 집합만을 다루므로 Union 연산은 합집한 연산과 같다.
•
Find: 하나읜 원소가 어떤 집합에 속해있는지를 판단한다.
크루스칼 알고리즘과 프림 알고리즘을 알기 위해선 유니온 파인드 알고리즘을 알아야 한다.
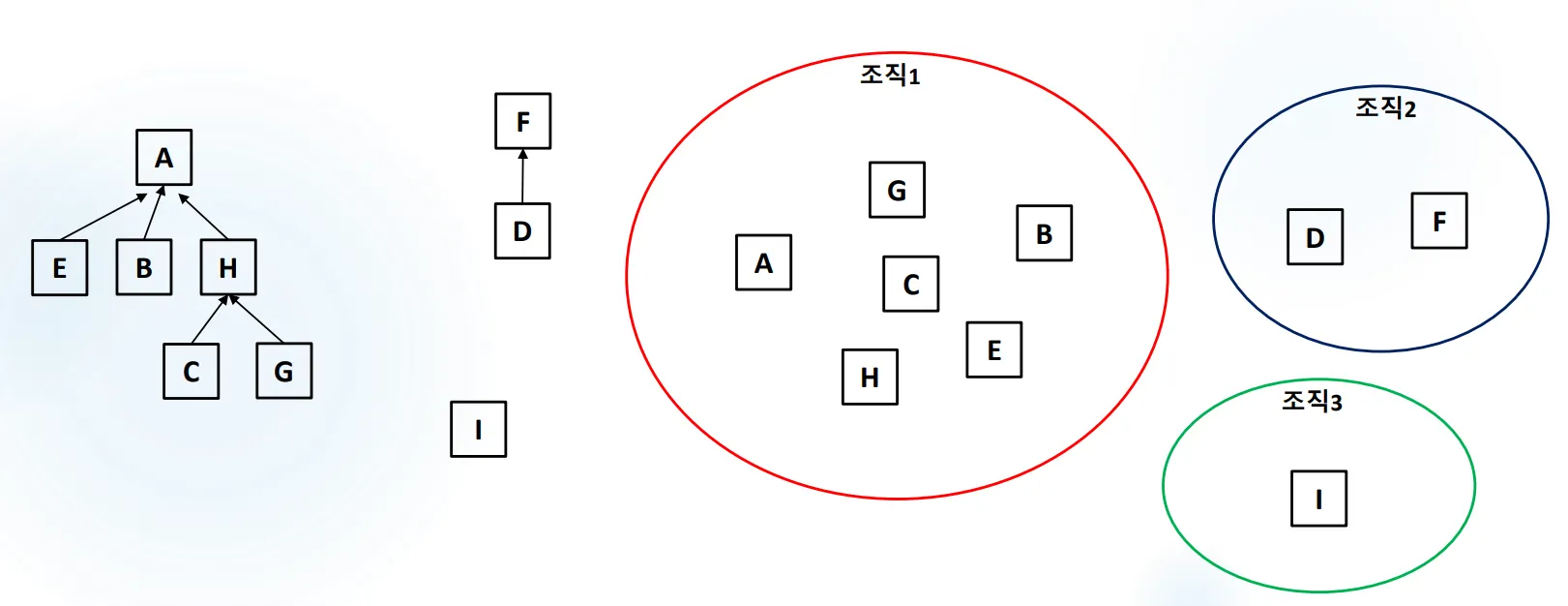
아래 그림은 각 데이터들을 총 3그룹으로 묶었다.
배열을 이용한 UnionFind Insert 구현해보기
#include <iostream>
#include <vector>
#include <list>
#include <string>
#include <algorithm>
#include <map>
int name[256] = {};
int n = 0;
int group[256] = {};
int gCnt = 0;
void insert(char ch1, char ch2)
{
//처음 등장한 문자라면, name 배열에 저장해 둔다
if (group[ch1] == 0)
name[n++] = ch1;
if (group[ch2] == 0)
name[n++] = ch2;
// a는 그룹에 있는데, b는 그룹에 없다.
if (group[ch1] != 0 && group[ch2] == 0)
group[ch2] = group[ch1];
// a그룹은 없고, b 그룹은 있다.
else if (group[ch1] == 0 && group[ch2] != 0)
group[ch1] = group[ch2];
//둘다 그룹이 없는경우는 새로운그룹을 만든다.
else if (group[ch1] == 0 && group[ch2] == 0)
{
gCnt++;
group[ch1] = gCnt;
group[ch2] = gCnt;
}
else
{
// 둘다 그룹이 있는 경우, 그룹을 a로 통합시킨다.
int g = group[ch2];
for (int i = 0; i < n; i++)
{
if (group[name[i]] == g)
group[name[i]] = group[ch1];
}
}
}
int main()
{
// 그룹으로 관리하는것은 분류하거나 검색하는데 있어서 유용하다.
// 그룹끼리 통합을 시키면 큰데이터를 연산하지 않고 작은 데이터로 연산할 수 있다.
// 그룹 1
insert('A', 'B');
insert('A', 'C');
// 그룹2
insert('E', 'Q');
insert('E', 'F');
// 통합
insert('F', 'A');
return 0;
}
C++
복사
재귀함수를 이용하여 UnionFind Insert구현해보기
#include <iostream>
#include <vector>
#include <list>
#include <string>
#include <algorithm>
#include <map>
char parent[1000];
char getParent(char x)
{
if (parent[x] == 0)
return x;
int ret = getParent(parent[x]);
parent[x] = ret;
return ret;
}
void BindGroup(char ch1, char ch2)
{
int a = getParent(ch1);
int b = getParent(ch2);
if (a != b)
parent[b] = a;
}
int main()
{
// 그룹으로 관리하는것은 분류하거나 검색하는데 있어서 유용하다.
// 그룹끼리 통합을 시키면 큰데이터를 연산하지 않고 작은 데이터로 연산할 수 있다.
BindGroup('A', 'G');
BindGroup('H', 'C');
BindGroup('A', 'H');
BindGroup('F', 'D');
BindGroup('A', 'F');
return 0;
}
C++
복사
“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.