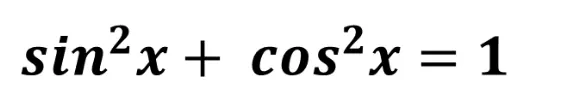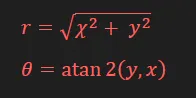각의 측정법
우리는 일상 생활에서 각Angle의 크기를 잴 때 0에서 360까지의 수를 사요하는 각도법Degree을 사욯한다.
각도법에서 기준으로 삼는 360이라는 수는 약수가 많아 원을 다양한 방법으로 쪼개어
활용할 수 있기 때문인데, 이는 일상생활의 편리를 위한 것일 뿐, 360이라는 값은 표준으로 사용하기에는 너무 큰 수이다.
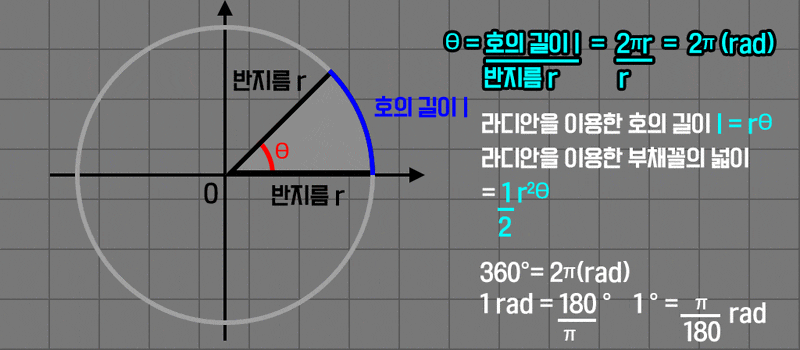
벡터의 경우 크기를 비교하기 용이하도록 크기 1의 단위 벡터를 정의한 것처럼 , 각을 측정할 때도 단위량 1을 기반으로 상대적인 크기를 측정할수 있도록 체계를 만들면 합리적일 것이다. 그래서 실무 계산에서 삼각함수를 응용 할 때에는 각도법 대신 호의 길이를 기준으로 각을 측정하는 방법을 사용한다.
이를 호도법(radian)이라고 한다. 호의 길이가 1이되는 부채꼴의 각을 기준으로 각을 측정한다.
삼각함수
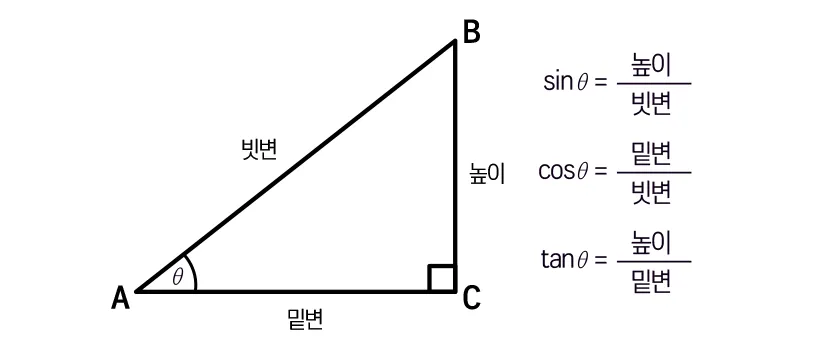
한 각이 90도인 직각삼감형을 이루는 세 변은 각 위치에 따라 빗변(직각의 대변), 밑변, 높이라고 부른다.
한 각이 직각이므로 나머지 두 각의 합이 90도가 되어야 한다. 따라서 두 각은 모두 90도보다 작은 예각이다.
직각 삼각형을 구성 하는 세 변에서 두변을 뽑아 각각의 비례관계를 나타낸 것을 삼각비 Trigonometric Ratio라고 한다. 삼각비에는 여러 종류가 있지만 sin, cosine, tangent 세가지가
가장 대표적이다.
가장 많이 사용하는 삼각함수인 sin함수와 cos함수의 개념은 직각삼각형에서 출발했지만,
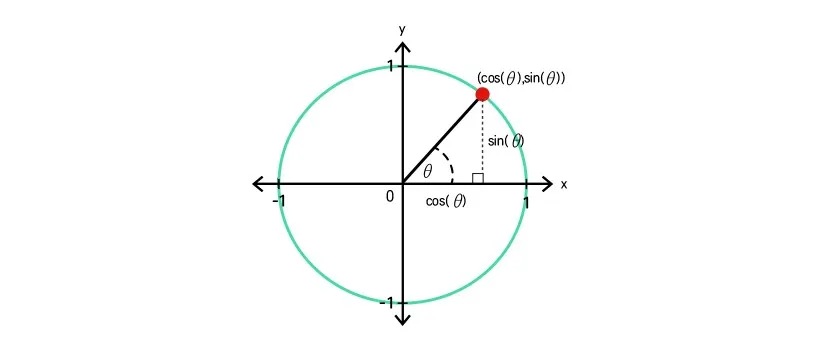
원점을 중심으로 반지름이 1인 평면위의 단위 원 (unit circle)을 사용해 나타내면 좀 더 쉽게 파악할 수 있다. 데카르트 좌표계에서 원점에서부터 1사분면의 단위 원의 원주 위에 있는 임의의 점을 이어 빗변을 그려보자.
그렇다면 밑변 a의 x좌표는 cos@ 가 되고 높이 b의 y 좌표는 sin@가 되는데 이를 피타고라스의 정리 a^2 = b^2 + c^2에 대입하면 다음과 같은 공식을 얻을 수 있다.
이 식은 삼각함수의 기본을 이루는 중요한 공식이므로, 이후 회전과 관련된 계산에 유용하게 사용 되므로 암기해두는 것을 권장한다.
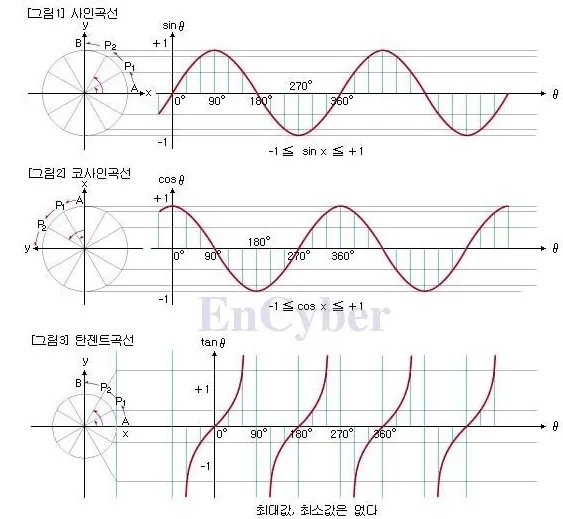
데카르트 좌표계에서 각도는 x축에서 원의 궤적을 따라 반시계 방향으로 회전한 크기를의미한다. 반지름이 1인 단위 원에서 반시계 방향의 회전을 생각해보자. 그래프를 그려보면 다음과 같다.
삼각함수의 역함수
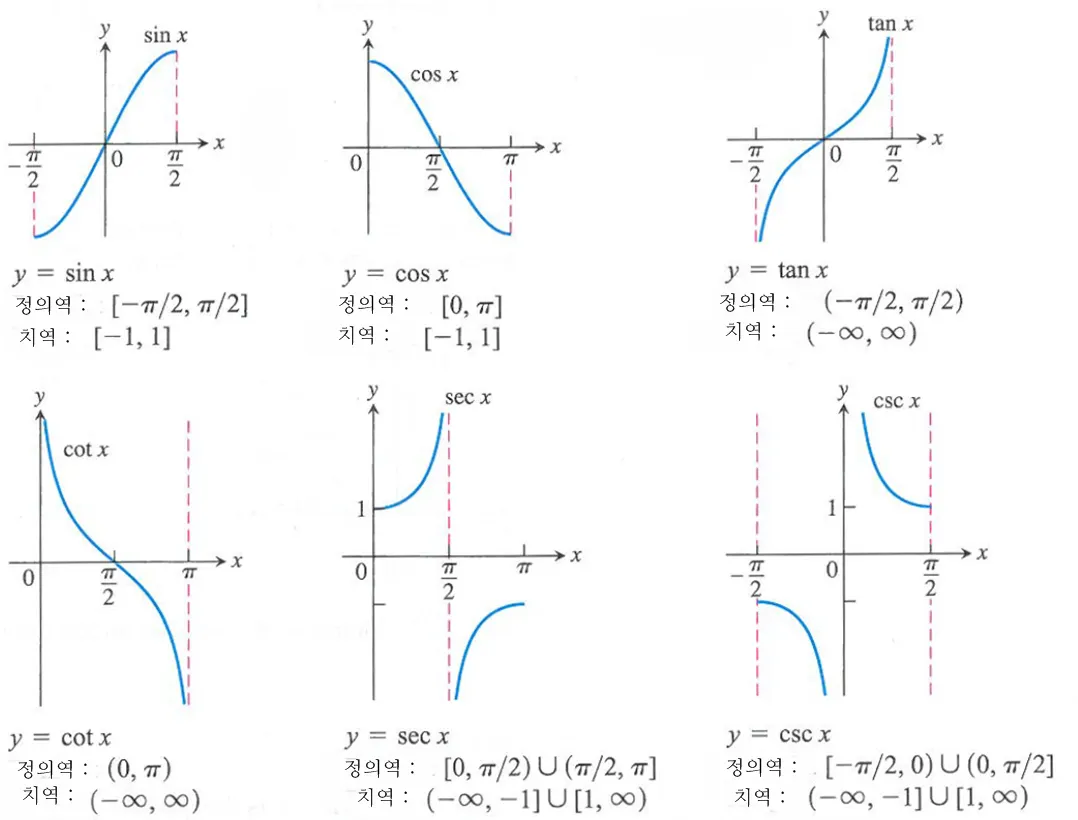
지금까지 삼각함수를 사용해 주어진 각에 대응하는 벡터의 좌표를 얻는 방법을 알아 보았다. 그런데 게임 제작 과정에서는 거꾸로 주어빈 벡터의 좌표로부터 이에 대응하는 각도를 얻어내는 작업도 필요하다. 이를 계산 하려면 삼각함수의 역함수와 이에대한 성질을 알아야 한다. 임의의 각 x에 대응되는 sin 함수는 다음과 같이 표기 할수 있다.
Tan의 역함수는 벡터의 각도를 구하는데 유용하게 사용된다.
임의의 벡터 (x,y)라고 할때 분수식 y/x 를 계산해 벡터로 부터 tan함수값을 얻을 수 있다.
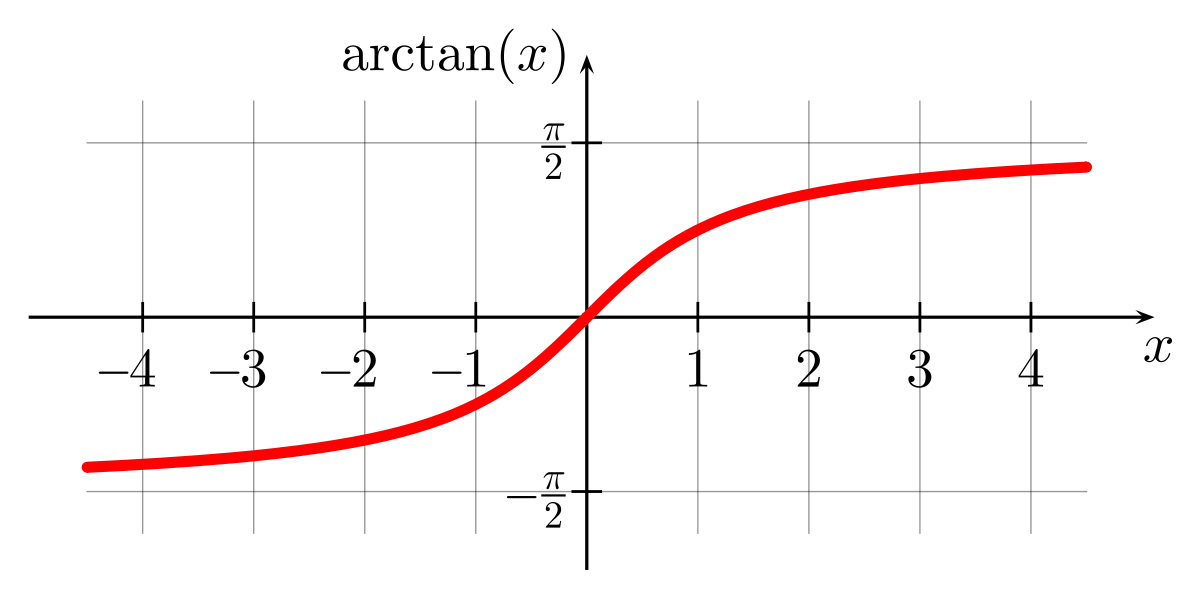
이tan값을 arctan 함수에 넣으면 해당 벡터가 x축과 이루는 사잇각을 얻어 낼 수 있다.
그런데 arctan함수의 치역(y의 범위)는 -90도 ~ 90도 이므로 arctan함수가 얻을수 있는 각의 범위는 한계가 있다. 이는arcsin함수와 arccos함수도 동일한 상황이다.
하지만 arctan함수의 경우 , 인자에 분수 y/x 를 넣지 않고 x와y의 두값을 분리해 전달하면 4사분면 전체에 해당하는 각의 정보를 얻을 수 있다. 예를 들어 x,y 가 둘다 음수인 경우를 생각해보자.
그런데 분수값 y/x 의 결과는 양수기 떄문에, arctan함수에 전달하면 3사분면의 정보는 사라지고
1사 분면에 해당하는 각의 정보가 나와 사용한 벡터를 얻어 낼 수가 없다.
하지만 arctan함수에 x와y 두 값을 따로 전달한다면 두 값이 가지는 부호를 파악해 벡터가 1사분면에 있었는지 3사분면에 있었는지 파악할 수 있다.
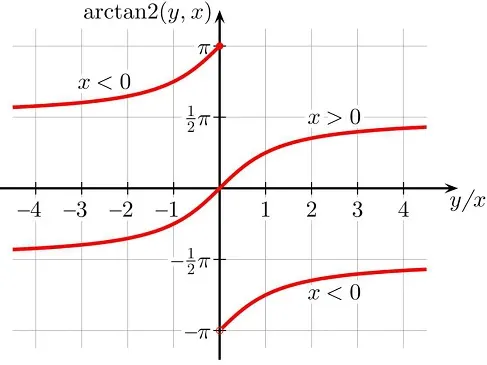
X, y를 따로 전달하는 arctan 함수를 atan2함수라고 부르며, 이는 분수 y/x 를 연상하기 쉽게 y값에 이어 x값을 전달하도록 설계 되어 있다. Atan2(y, x)
각의 크기를 x축으로 둔 atan2함수의 그래프는 다음과 같다.
극좌표계
물체를 이동시키고 크기를 늘리는 동작은 x와 y가 독점적으로 적용되는 움직임 인 데 반해, 회전은 x와 y가 함께 영양 받는 동작이라고 설명했다. 따라서 데카르트 좌표계로 회전을 구현하면 회전에 따른 x와 y 의 변화를 매번 계산하는 번거로움이 발생한다.
회전 동작을 기반으로 설계된 좌표계를 고안해 사용한다면, 이로부터 편리하게 회전을
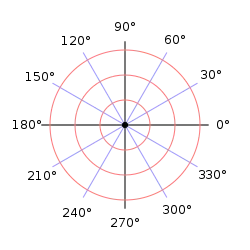
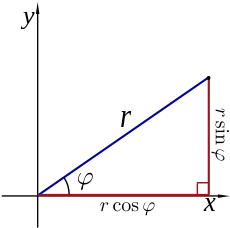
관리하고 구현 할 수 있을 것이다. 이를 위해 고안된 좌표계가 극좌표계 polar coordinate system이다. 극 좌표계는 원점으로부터의 거리 r과 각θ 두 요소로 구성되며 극 좌표계의 좌표는 (r, θ) 로 표시한다.
데카르트 좌표계로 표현된 벡터 (x,y)는 벡터의 크기와 arctan함수를 사용해 다음과 같이 극좌표계(r,θ)로 변환 할수 있다.
데카르트 좌표의 x와 y는 극좌표의 r로 변환할 수 있다.