다익스트라 알고리즘 (Dijkstra's Algorithm)
 핵심 개념
핵심 개념
재귀호출을 사용하지 않고 최단거리(최소비용) 구하는 알고리즘
최단거리 알고리즘들은 네트워크, 게임에서도 사용된다.
실생활 활용 예시
•
지하철 노선도 프로그램에서 최단경로를 찾는다던지
•
네트워크 사용 할때 최단경로로 연결을 구해야 한다던지
•
게임에서 캐릭터의 길찾기 알고리즘으로도 사용이 가능하다
 문제 예시
문제 예시
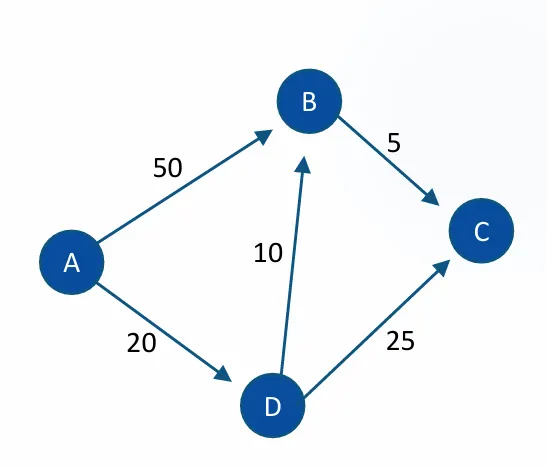
A에서 C까지 가는 최소 비용은?
A → D → B → C로 가면 총 35만원에 갈 수 있다.
그래프 구조:
B (5만원)
50↗ ↘5
A 10 C
20↘ ↗25
D
A→C 직접: 999999 (불가능)
A→D→B→C: 20 + 10 + 5 = 35만원 ✅ (최적)
Plain Text
복사
다익스트라 알고리즘을 통해서 A에서 출발해서 모든 도착지점의 최단경로를 구 할 수 있다.
 다익스트라 알고리즘 동작 원리
다익스트라 알고리즘 동작 원리
문제를 보면서 알아보자
A에서 C까지 가는 최소 비용은?
A → D → B → C로 가면 총 35만원에 갈 수 있다.
다익스트라 알고리즘을 통해서 A에서 출발해서 모든 도착지점의 최단경로를 구 할수 있다.
다음과 같은 규칙을 반복적으로 실행하면 최소비용을 구할 수 있다.
1.
가장 저렴하게 갈 수 있는 곳을 경유지로 선택한다.
2.
선택된 경유지를 거쳐 다른 곳으로 이동 할 때, 더 저렴한지 확인한다.
3.
더 저렴하다면, 최소비용 전광판에 갱신한다.
경유지로 한번 선택이 되었다면, 중복 방문체크를 위해서 배열에 체크해준다.
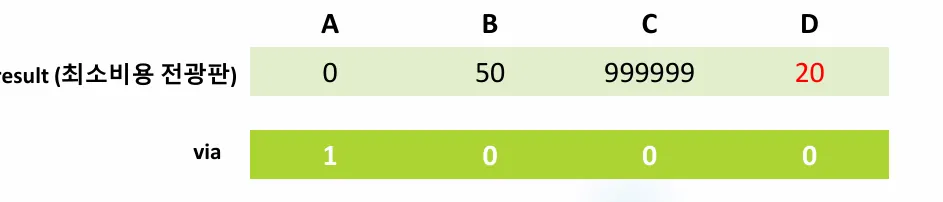
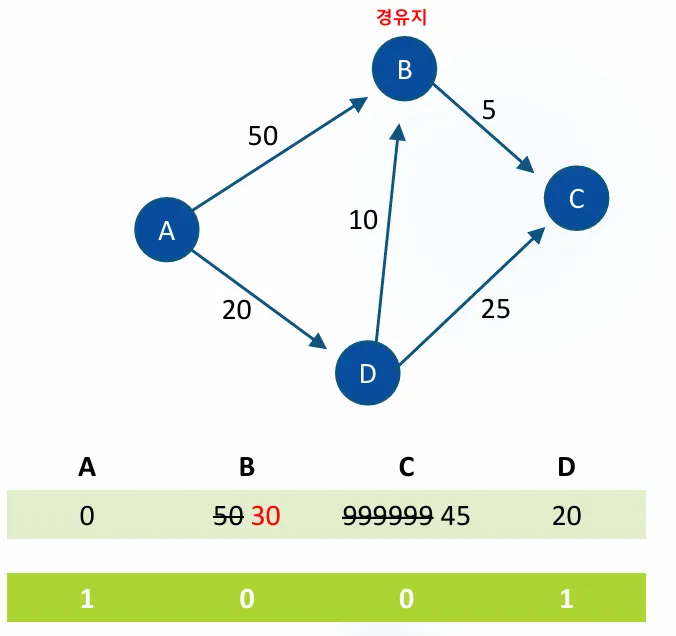
방문하지 않은 곳에서 가장 싼 값을 선택한다.
A에서 출발해서 D까지 가는 최소거리는 20이다.
D에서 들렸다가 다른지역 (A,B,C) 가는 비용
vs
전광판에 써있는 다른지역 (A,B,C)가는 비용
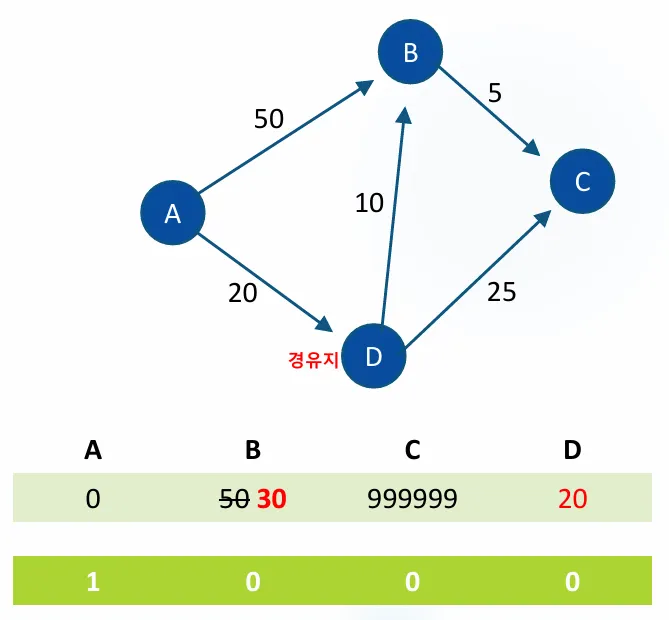
D에 들렸다가 B로 가는 비용 20 + 10 = 30
전광판에 써있는 B까지 가는비용은 50 이므로 전광판을 A→D→B = 30으로 수전한다.
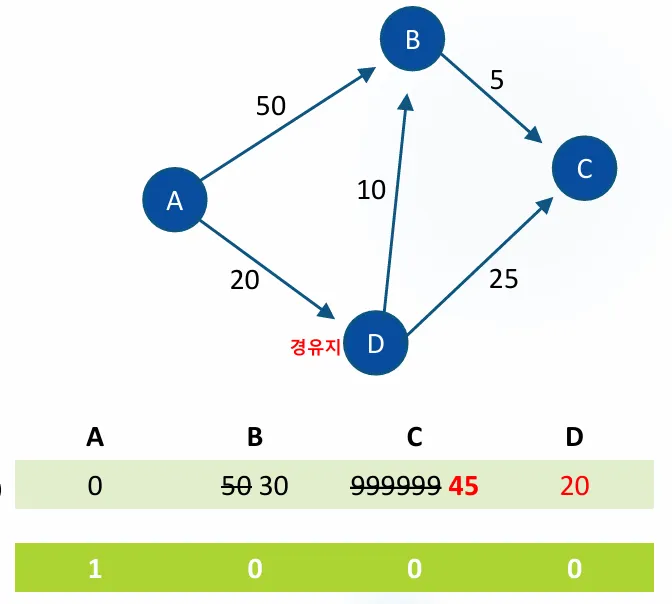
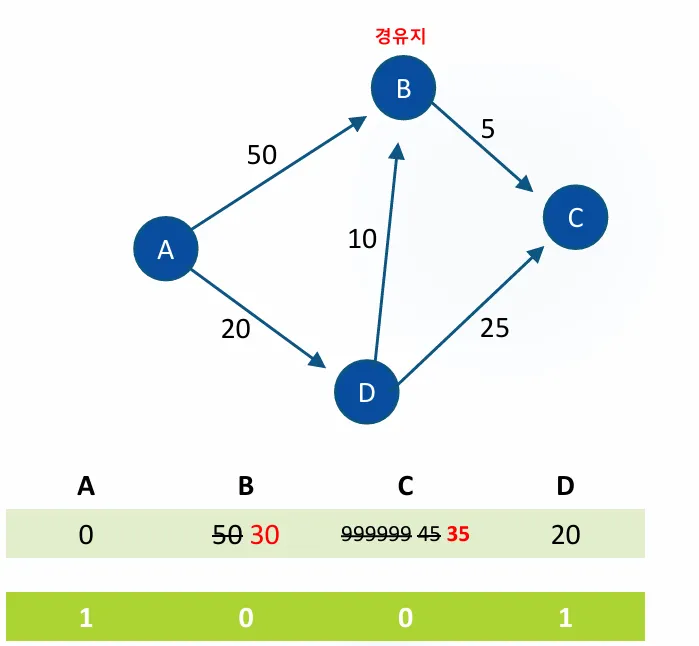
A에서 D를 들렸다가 C로 가는 비용은 20 + 25 = 45 이고
바로 A→C로가는 비용은 99999 이므로 값을 수정해준다. 더 싼 값으로
그러면 이제 D 를 거쳐서 가는 역할은 끝났다. D는 방문한곳으로 체크해준다. 중복 경유지를 제거해주기 위해서
이제 새로운 경유지를 통해서 다른 노드들의 비용을 계산하여 다시 비교해보자
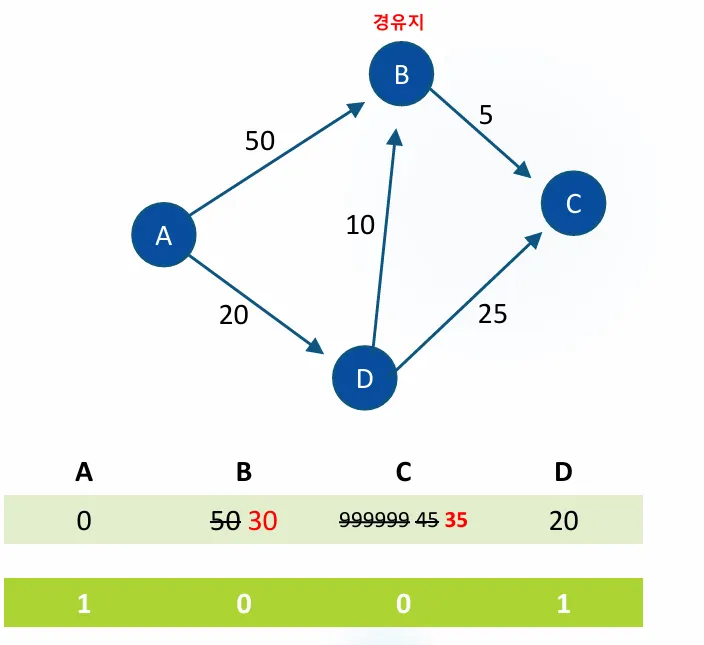
방문하지 않은곳 B를 들렸다가 C를 가는데 비용은
이미기록해둔 B경로값(30) + 5 = 35 이고 전광판에 써있는 C를 가는 비용은 45인데 이것보다 작으니 갱신해준다.
이런 과정을 반복하면 최정족으로 A>B : 30만원 A >C : 35만원 A>D 20
이렇게 최소비용을 구할 수 있다.
 다익스트라 알고리즘 완전 구현
다익스트라 알고리즘 완전 구현
#include <iostream>
#define NOT 999999
int map[4][4] = {
{0, 50, NOT, 20 }, // A에서 각 노드까지
{NOT, 0, 5, NOT}, // B에서 각 노드까지
{NOT, NOT, 0, NOT}, // C에서 각 노드까지
{NOT, 10, 25, 0 } // D에서 각 노드까지
};
int result[4] = {0, 50, NOT, 20}; // 최소비용 테이블
int visited[4] = {1, 0, 0, 0}; // 방문 여부 (A는 시작점이므로 방문됨)
// 방문하지 않은 노드 중 최소 비용 노드 찾기
int findMin()
{
int min = 987654321;
int minIndex = -1;
for (int i = 0; i < 4; i++)
{
if (visited[i] == 0 && result[i] < min)
{
min = result[i];
minIndex = i;
}
}
return minIndex;
}
void dijkstra()
{
int minIndex = 0;
for (int i = 0; i < 3; i++) // 3번 반복 (시작점 제외한 나머지 노드)
{
// 1. via가 0인 곳 중에 최소값을 찾기
minIndex = findMin();
// 2. a vs b 해서 a가 더 저렴하면 전광판에 갱신해준다.
// a = 경유지까지 가는 비용 + 경유지에서 목적지까지 가는 비용
// b = A에서 목적지까지 가는 비용
for (int j = 0; j < 4; j++)
{
int a = result[minIndex] + map[minIndex][j]; // 경유 비용
int b = result[j]; // 직행 비용
if (a < b)
{
result[j] = a; // 더 저렴하면 갱신
}
}
visited[minIndex] = 1; // 해당 노드 방문 완료
}
// 결과 출력
std::cout << "=== 최단 거리 결과 ===" << std::endl;
char nodes[] = {'A', 'B', 'C', 'D'};
for (int i = 0; i < 4; i++)
{
std::cout << "A → " << nodes[i] << ": " << result[i] << "만원" << std::endl;
}
}
int main() // char main()에서 int main()으로 수정
{
dijkstra();
return 0;
}
C++
복사
 알고리즘 핵심 로직 분석
알고리즘 핵심 로직 분석
1. findMin() 함수
// 방문하지 않은 노드 중 최소 비용 노드 찾기
int findMin() {
int min = 987654321;
int minIndex = -1;
for (int i = 0; i < 4; i++) {
if (visited[i] == 0 && result[i] < min) {
min = result[i];
minIndex = i;
}
}
return minIndex;
}
C++
복사
2. 거리 갱신 로직
// 경유지를 통한 비용 vs 직행 비용 비교
int a = result[minIndex] + map[minIndex][j]; // 경유 비용
int b = result[j]; // 현재 최소 비용
if (a < b) {
result[j] = a; // 더 저렴하면 갱신
}
C++
복사
 시간복잡도
시간복잡도
기본 다익스트라
•
시간복잡도: O(V²) - V는 정점의 개수
•
공간복잡도: O(V)
우선순위 큐 사용시
#include <queue>
#include <vector>
void dijkstra_optimized(int start)
{
vector<int> dist(V, INF);
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
dist[start] = 0;
pq.push({0, start});
while (!pq.empty()) {
int cost = pq.top().first;
int here = pq.top().second;
pq.pop();
if (dist[here] < cost) continue;
for (auto& edge : graph[here])
{
int there = edge.first;
int nextDist = cost + edge.second;
if (nextDist < dist[there])
{
dist[there] = nextDist;
pq.push({nextDist, there});
}
}
}
}
C++
복사
•
시간복잡도: O((V + E) log V) - 더 효율적
 다익스트라 vs 다른 최단경로 알고리즘
다익스트라 vs 다른 최단경로 알고리즘
알고리즘 | 시간복잡도 | 음수 가중치 | 모든 쌍 최단경로 |
다익스트라 | O(V²) 또는 O((V+E)logV) | ||
벨만-포드 | O(VE) | ||
플로이드-워셜 | O(V³) |
 실전 활용 예제
실전 활용 예제
1. 네비게이션 시스템
// 도로망에서 최단 경로 찾기
struct Road {
int to;
int distance;
int time;
};
void findShortestRoute(int start, int destination) {
// 다익스트라로 최단 경로 계산
}
C++
복사
2. 네트워크 라우팅
// 패킷이 가장 빠른 경로로 전송되도록
void findOptimalRoute(int source, int target) {
// 지연시간을 가중치로 하여 최적 경로 계산
}
C++
복사
3. 게임 AI 길찾기
// 캐릭터가 장애물을 피해 목적지까지
void findPath(Point start, Point goal) {
// 맵을 그래프로 변환하여 최단 경로 계산
}
C++
복사
 주의사항
주의사항
1. 음수 가중치 불가
다익스트라는 음수 가중치를 처리할 수 없습니다.
음수 가중치가 있다면 벨만-포드 알고리즘 사용!
Plain Text
복사
2. 그래프 표현
// 인접 행렬 vs 인접 리스트
int matrix[V][V]; // 메모리: O(V²), 밀집 그래프에 적합
vector<vector<pair<int,int>>> adj; // 메모리: O(V+E), 희소 그래프에 적합
C++
복사
3. 무한대 표현
#define INF 987654321 // 충분히 큰 값으로 설정
// 또는 #define INF INT_MAX 사용 (오버플로우 주의)
C++
복사
 핵심 정리
핵심 정리
다익스트라 알고리즘
1.
탐욕적 접근: 매번 최소 비용 노드 선택
2.
단일 출발점: 한 점에서 모든 점까지의 최단거리
3.
양수 가중치: 음수 가중치는 처리 불가
4.
실용적: 실제 최단경로 문제에 가장 많이 사용
핵심 단계
1.
초기화: 시작점 0, 나머지 무한대
2.
선택: 방문하지 않은 최소 비용 노드
3.
갱신: 선택된 노드를 통한 경로가 더 짧으면 갱신
4.
반복: 모든 노드 방문할 때까지
"가장 가까운 곳부터 차례대로 방문하며 최단거리를 확정짓는 알고리즘" 
“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.