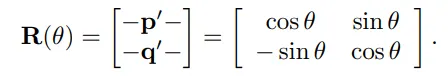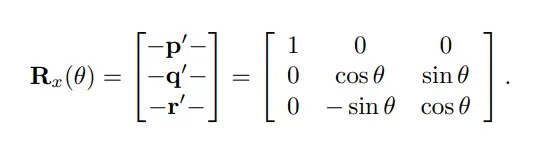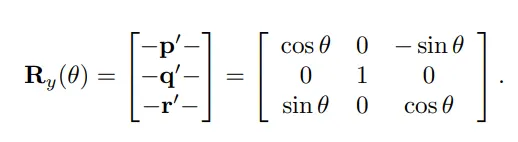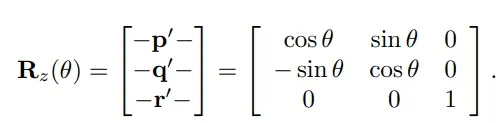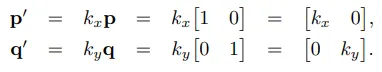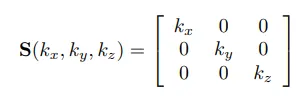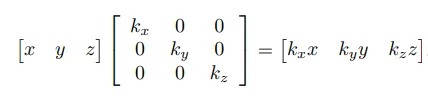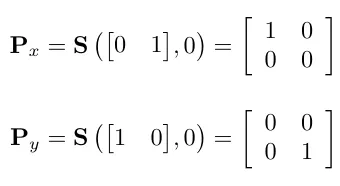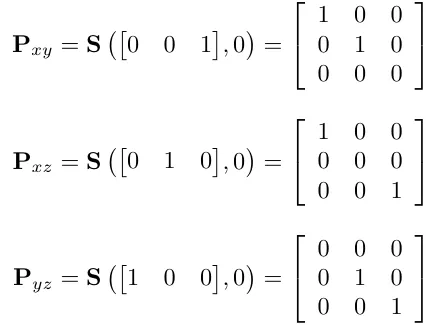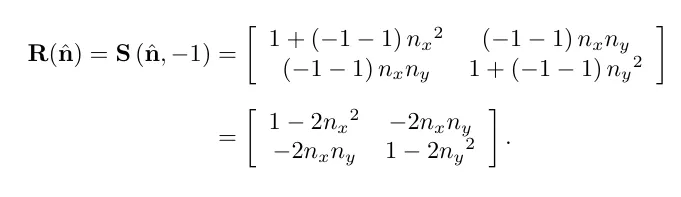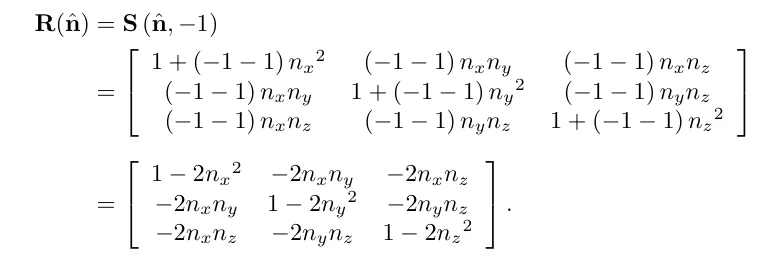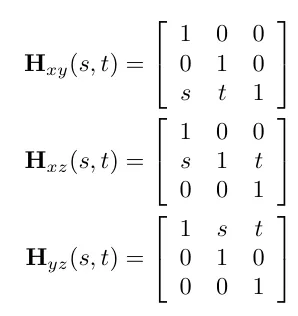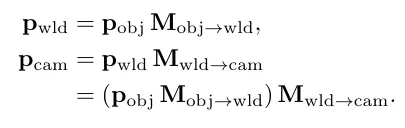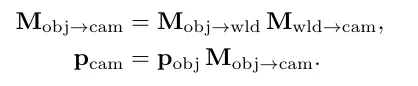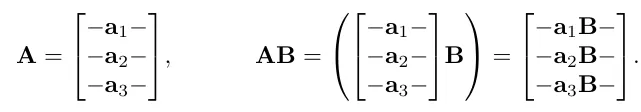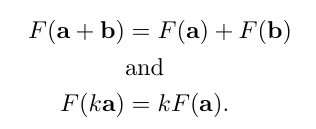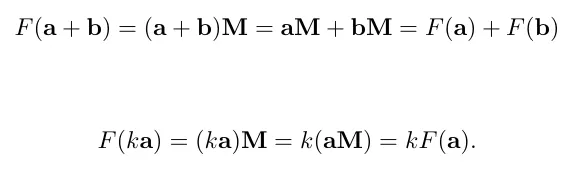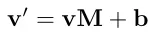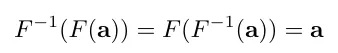우리는 앞에서 행렬과 기하학이 어떤 관계를 가지는지 학습 했습니다.
이번 장에서는 행렬이 선형 변환에서 어떻게 사용되는지 알아 볼 예정입니다.
행렬을 통한 선형변환 구현을 두 파트로 나눌수 있습니다. 이번 장에서 많은 공식과 세부사항들이 복잡하게 느껴질 수 있습니다. 간략하게 이해하고 넘어가고 싶은 마음은 굴뚝같지만 그러지 않는걸 추천합니다. 그렇다고 너무 세부 공식들을 외우실 필요는 없습니다.
해당 공식들을 기억하고 이해하고 필요 할때 다시 이장으로 돌아와서 참조하면 되기 떄문입니다.
회전(Rotation)
처음에는 간단하게 2D 공간상에서 회전 행렬 선형변환을 다루어 보겠습니다.
2D 공간산에서는 우리는 한가지 회전행렬만 신경쓰면 됩니다. 2D 좌표계에 존재하는 점을 회전시키면 됩니다.
여기서 우리가 주의 깊게 봐야할 점은 이 선형변환은 이동을 포함하지 않는 선형변환이라는 점 입니다. 2D 공간에서의 회전은 해당 점이 원점으로부터 오로지 하나의 값만을 이용해 회전을 표현합니다. 바로 각도( )입니다. 이것은 회전의 양을 표현하는 기호입니다.
기본적으로 각도에서는 반 시계 방향의 회전을 양수, 시계 방향의 회전을 음수로 표현합니다.
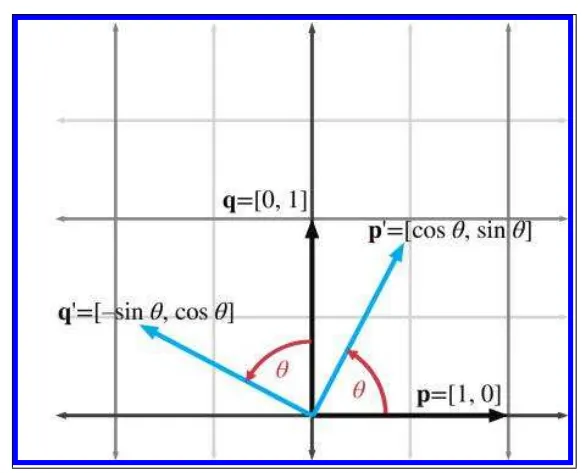
기저 벡터 p, q를 원점을 기준으로 회전시켜 만들어진 값을 p’, q’라고 하겠습니다.
회전을 표현하기 위한 미지수를 정했으니 이제 우리는 회전행렬을 만들 수 있습니다.
3차원 공간에서의 회전
3차원 공간에서 회전은 2차원 공간에서의 회전과 다르게 한 점이 어떤 축에 대해서 회전을 할것인지 표시해줘야 한다. 여기서 축이라는 용어는 x,y,z가 될수 있고 또한 x,y, 또는 z축 하나만 지정이 될 수 있습니다.
3차원 공간에서 회전을 할떄 좌표계에 따라서 방향이 달라 질 수 있습니다. 우리는 왼손좌표계를 기준으로 회전 시키겠습니다.
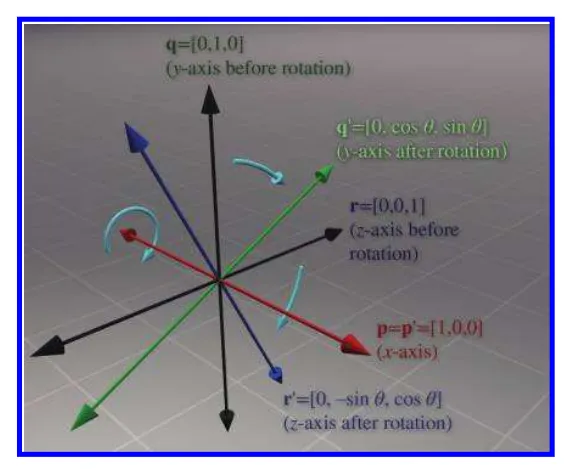
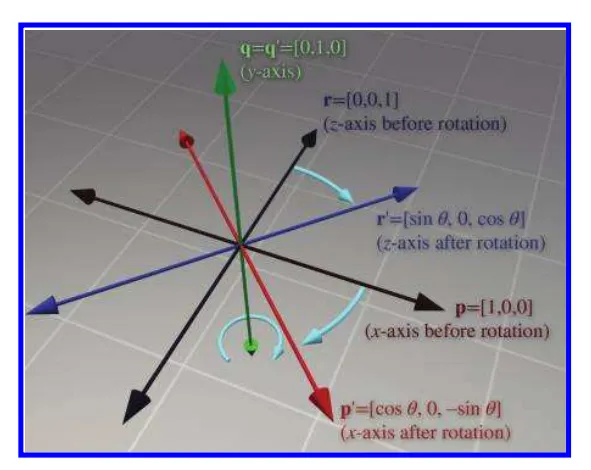
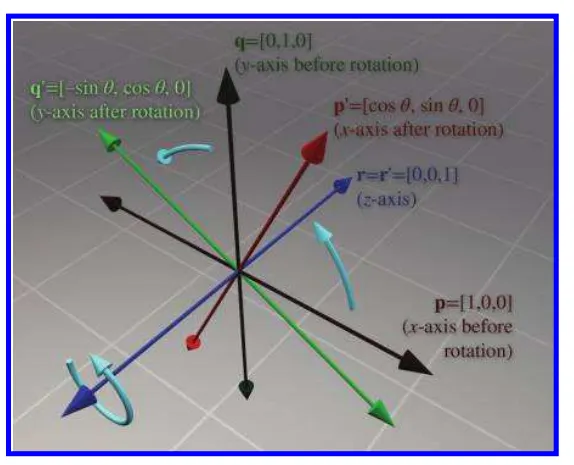
2차원 좌표계와 마찬가지로 3차원 좌표를 각각 p,q,r 회전된 좌표를 p’,q’,r’ 이라고 하겠습니다.
x축에 대한 회전 행렬은 다음과 같이 구성할 수 있습니다.
y축에 대한 회전 행렬은 다음과 같이 구성 할 수 있습니다.
z축에 대한 회전행렬은 다음과 같이 구성 됩니다.
3D 공간에서 임의의 축에 대한 회전
크기 (Scale)
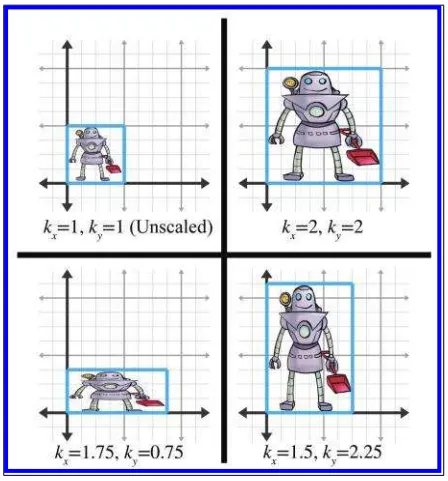
우리는 오브젝트의 크기도 행렬을 통해서 늘리거나 줄이거나 할 수 있습니다.
가장 간단하게 물체의 크기를 조정하는 방법은 각 축마다 조정하는 것 입니다.
2차원이든 3차원이든 각축에 대한 스케일 변환 연산만 진행해주면 됩니다.
p,q에서 스케일변환된 좌표를 p’, q’ 라고하면 이는 벡터에 스칼라배를 곱하거와 같습니다.
이를 통해서 행렬을 유도시켜볼 수 있습니다.
3차원으로 확장시키면 다음과같이 만들수 있습니다.
임의의 축 스케일 변환
직교 투영 (Orthographic Projection)
일반적으로 투영이라는 말은 차원을 축소시키는 용어입니다.
직교 투영은 거리에 상관없이 3차원 을 2차원으로 투영 시키는 방법입니다. 모든 정점과 평면에 픽셀은 평행합니다.
투영 변환을 할때 단순히 좌표계 하나를 버리고 z를 버리고 x,y만 가지고 만들어서 3D개체를 2D개체를 바꿀수 있습니다.
기본축에 투영(2차원 → 1차원)
평면에 투영(3차원 → 2차원)
임의의 축, 평면의 투영
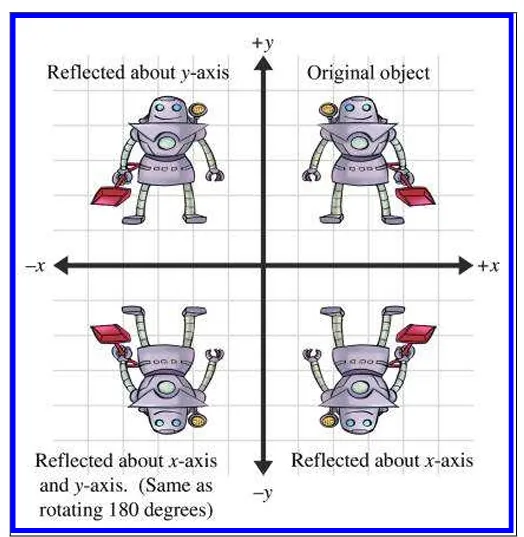
반사 (Reflection)
반사행렬은 미러링이라고도 불립니다. 오브젝트를 2D,3D상에서 뒤집는거라고 보시면 됩니다.
반사행렬은 스케일 행렬에서 -1 연산을 해주는것으로 만들수 있습니다.
매우 간단합니다.
2D행렬에서의 반사 행렬
3D 행렬에서의 반사 행렬
Shearing(전단)
전단 변환은 기울이고 늘리는 변환입니다. 그래서 각도가 유지되지 않습니다. 그렇다고 해도 면적은 바뀌지 않습니다. 만드는 방법은 매우 간단합니다.
Hxy 는 y축 좌표에 따라 x축 방향으로 전단을 조절하는 행렬입니다.
전단행렬은 거의 사용되지 않는 행렬중 하나입니다 간단한 원리와 예시만 보고 넘어가도 좋습니다.
Combining Transformations(행렬 간 결합)
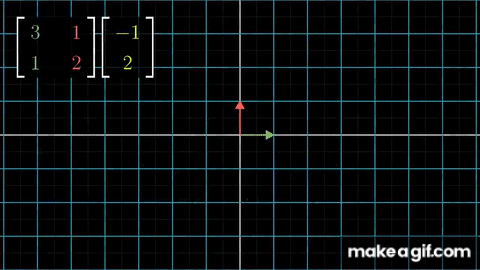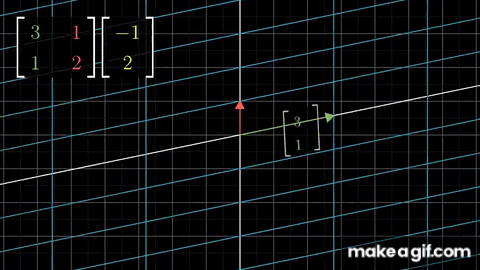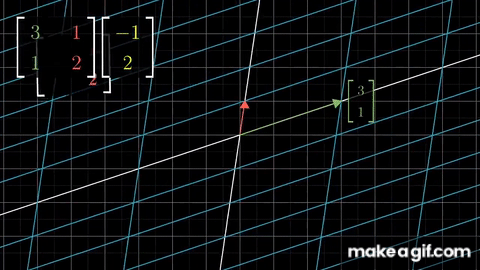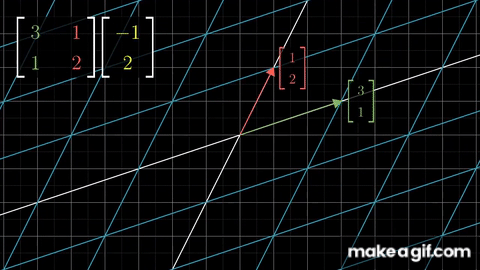
이번에는 여러 행렬들을 겹합하여 하나의 행렬로 만드는 방법을 보여줍니다. 이 단일행렬은 여러개의 행렬을 순서대로 적용한 누적 결과를 나타냅니다. 행렬 A와 행렬 B를 사용하여 변환을 적용한 결과 AB 행렬이 있습니다.
일반적인 예시는 특정 오브젝트가 World공간에 물체가 있다고 상상해봅시다. 우리는 카메라를 통해서 이 물체를 렌더링 하고 싶습니다. 우리는 오브젝트의 모든 정점을 월드 공간으로 변환해야 합니다. 그리고 해당 월드에 있는 모든 정점을 다시 카메라 공간으로 옮겨야 합니다.
관련된 행렬 간 결합을 수학적으로 표현하면 다음과 같이 표현이 가능합니다.
월드행렬과 뷰행렬의 곱을 통해서 만들어진 단일행렬으로 오브젝트의 정점들을 카메라공간으로 변환 할 수있는 행렬을 만들 수 있습니다.
따라서 최종적으로 만들어진 행렬 하나만을 통해서 각정점에 위치를 로컬 → 월드 → 카메라 공간으로 한번에 변환 시 킬 수 있습니다.
따라서 행렬의 연결은 행렬 곱셈의 연속속성을 사용 하는 것입니다. 무슨 일이 일어나는지 조금 더 기하학적인 관점에서 보겠습니다. 우리는 앞서 행렬에 행이 기저벡터의 변환을 위한 결과가 포함되어 있는 걸 배웠습니다. 두 행렬의 곱으로 만들어진 행렬은 기본적으로 서로 다른 두행렬의 기저벡터의 연속적인 곱을 표현합니다.
AB 행렬이 A의 기저벡터를 B로 변환한 결과임을 볼수 있습니다.
그말인 즉슨 두 행렬의 곱은 각각의 행렬간 기저벡터의 변환을 연속적으로 시행하는 것과 같습니다.
선형변환(Linear Transformations)
수학적으로 다음과 같은 공식이 성립할때 선형변환이 성립됩니다.
위 F를 우리는 행렬을 사용하여 치환할수 있습니다.
앞에서 배운 모든 변환은 행렬의 곱셉을 사용하여 표현 할 수 있습니다. 그러므로 선형변환이 성립됩니다. 선형 변환은 변환후에도 원점은 그대로 유지되기 떄문에 대립선이 평행하게 유지되는 것을 알 수 있습니다.
이것은 두 가지 예외가 있습니다.
1. 평행 이동은 선형 변환이 아닙니다.
•
*평행 이동(Translation)**은 모든 점을 일정한 벡터만큼 이동시키는 변환입니다. 예를 들어, 2차원 공간에서 벡터 v만큼 모든 점을 이동시키는 경우입니다. 평행 이동은 다음과 같이 정의됩니다:
그러나 평행 이동은 선형 변환이 아닙니다. 그 이유는 선형 변환의 핵심 속성 중 하나인 원점을 원점으로 보낸다는 조건을 만족하지 않기 때문입니다. 선형 변환 TTT에 대해 이어야 하지만, 평행 이동의 경우:
따라서 평행 이동은 선형 변환이 아닌 **아핀 변환(Affine Transformation)**입니다. 아핀 변환은 선형 변환에 평행 이동을 추가한 형태로, 선형 변환의 성질 일부를 공유하지만 완전히 동일하지는 않습니다.
그러나, 평행 이동은 평행성을 보존합니다. 즉, 평행한 선분이나 직선은 평행 이동 후에도 여전히 평행합니다. 이는 아핀 변환의 성질 중 하나로, 평행성을 유지하지만 선형성은 유지하지 않습니다.
2. 투영에서의 평행선과 점의 관계
•
*투영(Projection)**은 공간의 한 부분을 다른 부분으로 사상하는 변환으로, 예를 들어 고차원 공간의 점을 저차원 공간으로 투영하는 것입니다. 투영에는 주로 두 가지 유형이 있습니다:
1.
직교 투영(Orthogonal Projection): 특정 축 또는 평면에 수직인 방향으로 투영하는 것.
2.
원근 투영(Perspective Projection): 시점(Vanishing Point)을 향해 투영하는 것.
질문에 대한 답변:
•
선이 투영되어 단일 점이 되는 경우, 이는 원근 투영에서 발생할 수 있는 현상입니다. 예를 들어, 3차원 공간에서 무한히 먼 평행한 선들이 한 점으로 모이는 것처럼 보이는 것입니다. 이는 소위 **소실점(Vanishing Point)**의 개념과 관련이 있습니다.
•
그러나 투영 후 점이 된 선과 원래의 평행선 사이에 평행성을 직접적으로 정의하기는 어렵습니다. 왜냐하면 투영 과정에서 차원이 감소하면서 평행선의 개념이 사라지기 때문입니다.
•
평행성은 동일한 차원에서 정의되는 개념입니다. 따라서 선(1차원)이 점(0차원)으로 변환된 경우, 그 사이의 평행성을 논의하기 위해서는 추가적인 구조나 맥락이 필요합니다.
요약하면:
•
투영 변환에서 선이 점으로 사상될 수 있지만, 이때 그 점을 원래의 평행선과 평행하다고 보기는 어렵습니다.
•
대신, 투영 변환이 어떤 성질을 보존하는지에 따라 이해해야 합니다. 예를 들어, 직교 투영은 거리를 단축하지만 평행성을 보존하며, 원근 투영은 평행선을 소실점으로 모이게 하지만 실제로는 평행성을 왜곡합니다.
애파인 변환(Affine Transformations)
아핀변환은 선형변환이 이루어진후 이동변환이 진행됩니다. 따라서
아핀변환은 선형변환을 포함하는 상위변환 입니다. 모든 선형변환은 아핀변환이지만 아핀변환은 선형변환이 아닙니다. 우리가 앞서 배웠던 모든 변환은 선형변환 이었습니다. 하지만 모두 아핀변환에 포함될수도 있습니다. 수학적으로 다음과 같이 표시 할 수도 있습니다.
역변환(Invertable Transformations)
역변환이란 행렬의 변환이 이루어지고 나서 다시 그 변환을 역으로 돌리 수 있는 경우를 이야기 합니다.
Angle-Preserving Transformations (각도 보존 변환)
Angle-Preserving Transformations는 변환 후에도 두 벡터 간의 각도를 유지하는 변환을 말합니다. 수학적으로 이 변환은 유클리드 공간에서 벡터 간의 각도를 변화시키지 않는다는 특징이 있습니다. 이런 변환은 다음과 같은 성질을 갖습니다:
•
두 벡터 u와 v가 변환 전후에도 각도가 동일하게 유지됩니다. 즉, 변환 후의 벡터 T(u)와 T(v) 간의 각도는 변환 전 벡터 u와 v 간의 각도와 동일합니다.
•
*회전(rotation)**과 같은 변환이 이 범주에 속합니다. 벡터의 크기를 유지하면서 각도를 보존합니다.
Orthogonal Transformations (직교 변환)
Orthogonal Transformations은 선형 변환 중에서 변환 후에도 벡터 간의 **직교성(orthogonality)**이 유지되는 변환을 말합니다. 수학적으로는 직교 행렬을 사용하여 표현되며, 다음과 같은 특징이 있습니다:
•
행렬 A가 직교 행렬(orthogonal matrix)일 때, ATA=I (단위 행렬) 조건을 만족합니다. 여기서 AT는 행렬 A의 전치 행렬입니다.
•
이 변환은 벡터 간의 각도와 길이를 유지하며, 주로 **회전(rotation)**이나 **반사(reflection)**가 직교 변환의 예시입니다.
•
특징: 직교 변환은 크기를 변화시키지 않으므로 벡터의 길이(norm)가 보존됩니다.
Rigid Body Transformations (강체 변환)
Rigid Body Transformations은 공간에서 **강체(강성체, Rigid Body)**가 변형 없이 이동하거나 회전하는 변환을 말합니다. 이러한 변환에서는 객체의 모양이나 크기가 변하지 않고, 단지 위치나 방향만 바뀝니다. 이를 강체 운동이라고도 합니다.
•
*회전(rotation)**과 **이동(translation)**이 포함된 변환입니다. 강체 변환에서는 변환 전후에 두 점 사이의 거리가 변하지 않습니다.
•
특징: 각도와 거리 모두가 보존됩니다.
•
강체 변환은 로봇 공학이나 기계공학에서 매우 중요한 역할을 하며, 물리학에서 강체의 운동을 설명하는 데 사용됩니다
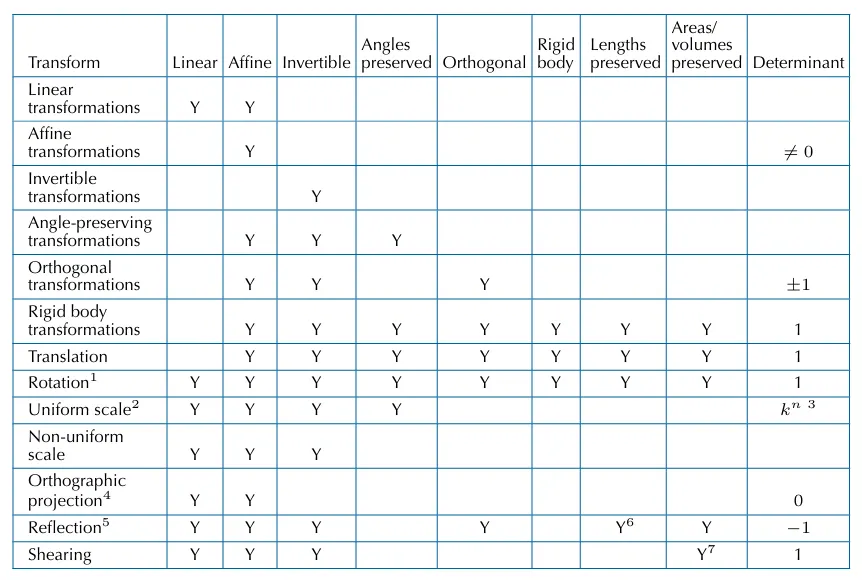
최종적으로 각각의 변환을 표를 통해서 어떤변환에 포함되는지 요약한 표를 제공하겠습니다.