정렬 알고리즘 시간복잡도 비교
정렬 알고리즘 | 시간복잡도 |
선택정렬 | n^2 |
삽입정렬 | n^2 |
버블정렬 | n^2 |
병합정렬 | nlogn |
힙정렬 | nlogn |
퀵정렬 | nlogn |
트리정렬 | nlogn |
팀정렬 | nlogn |
핵심 개념: 특정 정렬 알고리즘이 무조건 좋다는 개념은 없습니다. 원소의 개수, 사용 가능한 메모리 크기, 데이터의 초기 상태(정렬 여부, 중복 원소 비율 등)를 모두 고려해야 합니다. 경우에 따라 단순한 버블정렬이나 삽입정렬이 더 효율적일 수 있습니다.
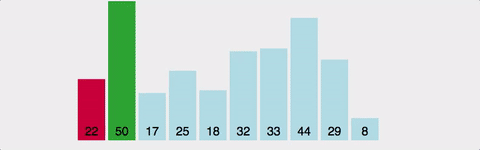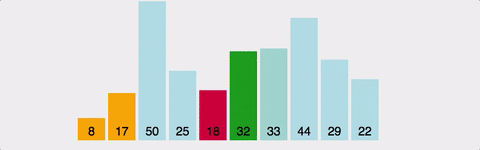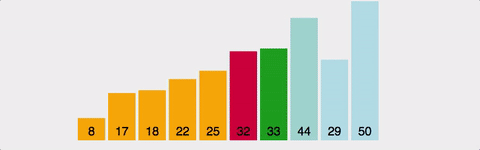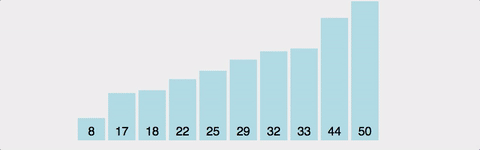
선택정렬 (Selection Sort)
한 줄 요약
"매번 가장 작은 값을 찾아서 앞으로 보낸다"
핵심 아이디어
선택정렬은 이름 그대로 선택해서 정렬합니다:
1.
전체에서 가장 작은 값을 선택
2.
맨 앞과 교환
3.
다음 위치에서 반복
예시: 줄을 세울 때 매번 가장 키 작은 사람을 찾아서 앞으로 보내는 것과 같습니다!
단계별 동작 과정
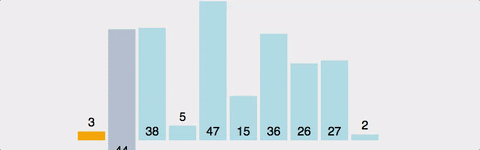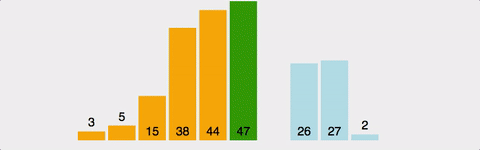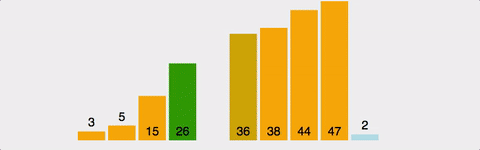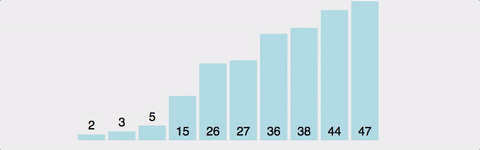
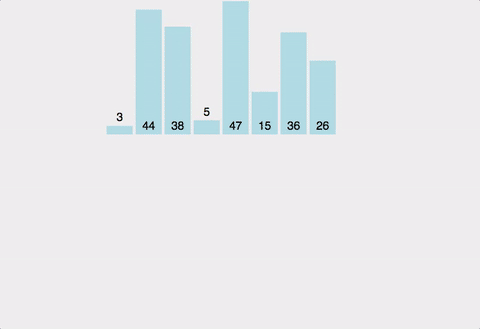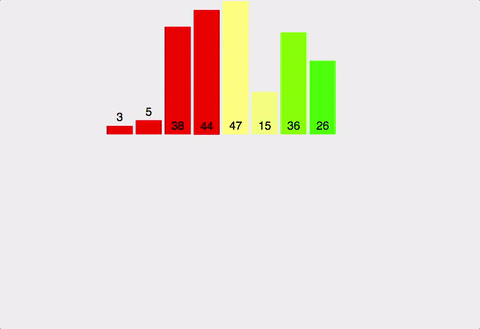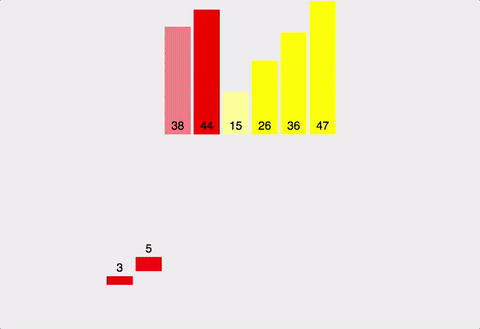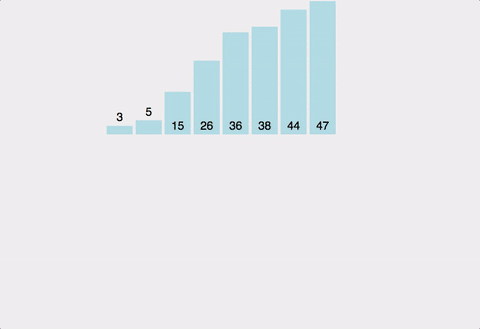
예시 배열: [5, 3, 8, 1, 2, 7]
1단계: 전체에서 최솟값 1 찾기
•
전체 배열을 순회하며 최솟값 1을 찾습니다
•
첫 번째 위치(5)와 최솟값(1)을 교환합니다
•
결과: [1, 3, 8, 5, 2, 7] ✓
2단계: 두 번째부터 최솟값 2 찾기
•
인덱스 1부터 끝까지 순회하며 최솟값 2를 찾습니다
•
두 번째 위치(3)와 최솟값(2)을 교환합니다
•
결과: [1, 2, 8, 5, 3, 7] ✓✓
3단계: 세 번째부터 최솟값 3 찾기
•
인덱스 2부터 끝까지 순회하며 최솟값 3을 찾습니다
•
세 번째 위치(8)와 최솟값(3)을 교환합니다
•
결과: [1, 2, 3, 5, 8, 7] ✓✓✓
4단계: 네 번째부터 최솟값 5 찾기
•
인덱스 3부터 끝까지 순회하며 최솟값 5를 찾습니다
•
현재 위치가 이미 최솟값이므로 교환하지 않습니다
•
결과: [1, 2, 3, 5, 8, 7] ✓✓✓✓
5단계: 다섯 번째부터 최솟값 7 찾기
•
인덱스 4부터 끝까지 순회하며 최솟값 7을 찾습니다
•
다섯 번째 위치(8)와 최솟값(7)을 교환합니다
•
결과: [1, 2, 3, 5, 7, 8] ✓✓✓✓✓
6단계: 정렬 완료
•
마지막 원소는 자동으로 정렬되므로 확인할 필요가 없습니다
•
정렬 완료! ✓✓✓✓✓✓
왜 이렇게 동작할까?
매 단계마다:
•
남은 부분에서 최솟값을 찾습니다 (선형 탐색)
•
찾은 값을 현재 위치와 교환합니다
•
현재 위치는 이제 확정! 다시 건드리지 않습니다
시간복잡도
•
모든 경우: O(n²)
•
이미 정렬되어 있어도 O(n²)
•
역순이어도 O(n²)
이유: 매번 남은 전체를 다 뒤져서 최솟값을 찾아야 하기 때문입니다.
선택정렬 구현 코드
void selectionSort(std::vector<int>& arr)
{
int n = arr.size();
// 배열의 처음부터 끝에서 두 번째까지 반복
// (마지막 원소는 자동으로 정렬되므로 n-1까지만)
for (int i = 0; i < n - 1; i++)
{
int minIndex = i; // 현재 위치를 최솟값 인덱스로 초기화
// 현재 위치 다음부터 배열 끝까지 순회하며 최솟값 찾기
for (int j = i + 1; j < n; j++)
{
if (arr[j] < arr[minIndex])
{
minIndex = j; // 더 작은 값을 발견하면 인덱스 갱신
}
}
// 최솟값이 현재 위치가 아니라면 교환
// (이미 최솟값이 현재 위치에 있다면 불필요한 교환 방지)
if (minIndex != i)
{
std::swap(arr[i], arr[minIndex]);
}
}
}
C++
복사
코드 상세 설명:
•
외부 루프 (i): 정렬될 위치를 나타냅니다. 0부터 n-2까지 반복합니다.
•
내부 루프 (j): i+1부터 끝까지 순회하며 최솟값의 인덱스를 찾습니다.
•
minIndex: 현재까지 발견한 최솟값의 인덱스를 저장합니다.
•
swap: 최솟값을 현재 위치로 이동시킵니다.
동작 과정 단계별 분석
초기 배열: [64, 25, 12, 22, 11]
1단계: i=0, 전체 배열에서 최솟값 11 찾기
•
비교: 64와 25, 25와 12, 12와 22, 22와 11
•
최솟값: 11 (인덱스 4)
•
교환: 64  11
11
•
결과: [11, 25, 12, 22, 64]
2단계: i=1, 인덱스 1부터 끝까지 중 최솟값 12 찾기
•
비교: 25와 12, 12와 22, 12와 64
•
최솟값: 12 (인덱스 2)
•
교환: 25  12
12
•
결과: [11, 12, 25, 22, 64]
3단계: i=2, 인덱스 2부터 끝까지 중 최솟값 22 찾기
•
비교: 25와 22, 22와 64
•
최솟값: 22 (인덱스 3)
•
교환: 25  22
22
•
결과: [11, 12, 22, 25, 64]
4단계: i=3, 인덱스 3부터 끝까지 중 최솟값 25 찾기
•
비교: 25와 64
•
최솟값: 25 (인덱스 3, 이미 제자리)
•
교환: 없음
•
결과: [11, 12, 22, 25, 64]
정렬 완료!
장단점
•
간단명료: 코드가 정말 짧고 이해하기 쉽습니다
•
메모리 효율: 추가 메모리가 전혀 필요 없습니다
•
교환 횟수 적음: 최대 n-1번만 교환 (비교는 많이 하지만 교환은 적음)
•
예측 가능: 어떤 데이터든 성능이 똑같습니다
•
느립니다: 데이터가 많으면 매우 느립니다 (O(n²))
•
최적화 불가: 이미 정렬되어 있어도 처음부터 끝까지 다 확인합니다
•
실무에서는 거의 안 씁니다: 학습용으로만 좋습니다
언제 쓸까요? 데이터가 매우 적고(10개 미만), 코드를 최대한 간단하게 짜고 싶을 때!
삽입정렬 (Insertion Sort)
한 줄 요약
"카드 정리하듯이 하나씩 적절한 위치에 끼워 넣는다"
핵심 아이디어
트럼프 카드를 정리할 때를 생각해보세요:
1.
첫 번째 카드는 그냥 둡니다 (이미 정렬됨)
2.
두 번째 카드를 받으면 첫 번째와 비교해서 끼워 넣습니다
3.
세 번째 카드를 받으면 앞의 정렬된 카드들 사이에 끼워 넣습니다
4.
이렇게 계속...
핵심: 왼쪽은 항상 정렬된 상태를 유지하면서, 새 카드를 적절한 위치에 삽입합니다!
단계별 동작 과정
예시 배열: [5, 2, 4, 6, 1, 3]
초기 상태
1단계: 2를 삽입
2단계: 4를 삽입
3단계: 6을 삽입
4단계: 1을 삽입
5단계: 3을 삽입
왜 이렇게 동작할까?
핵심 원리:
•
현재 원소를 key로 저장
•
왼쪽으로 가면서 key보다 큰 값들을 오른쪽으로 밀어냅니다
•
적절한 위치를 찾으면 key를 삽입
시간복잡도
•
최선: O(n) ← 이미 정렬된 경우 (대박!)
•
평균: O(n²) ← 무작위 데이터
•
최악: O(n²) ← 역순 정렬
왜 최선이 O(n)일까?
이미 정렬되어 있으면 각 원소마다 바로 앞 원소 하나만 확인하고 끝!
이것이 삽입정렬의 최대 강점입니다!
삽입정렬 구현 코드
void insertionSort(std::vector<int>& arr)
{
// 두 번째 원소부터 시작 (첫 번째 원소는 이미 정렬된 것으로 간주)
for (int i = 1; i < arr.size(); i++)
{
int key = arr[i]; // 현재 삽입할 원소를 key에 저장
int j = i - 1; // 정렬된 부분의 마지막 인덱스
// key보다 큰 원소들을 한 칸씩 뒤로 이동
// j가 0 이상이고, arr[j]가 key보다 크면 계속 이동
while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j]; // 한 칸 뒤로 이동
j--; // 왼쪽으로 이동하며 계속 비교
}
// while 루프가 종료된 위치(j+1)에 key 삽입
arr[j + 1] = key;
}
}
C++
복사
코드 상세 설명:
•
i 루프: 삽입할 원소의 위치입니다. 1부터 시작하는 이유는 첫 번째 원소(인덱스 0)는 이미 정렬된 것으로 봅니다.
•
key: 현재 삽입하려는 값입니다.
•
j: 정렬된 부분을 역순으로 탐색하는 인덱스입니다.
•
while 루프: key보다 큰 값들을 오른쪽으로 한 칸씩 이동시킵니다.
장단점
•
거의 정렬된 데이터에 최적: O(n)까지 빨라집니다!
•
온라인 정렬 가능: 데이터가 하나씩 들어올 때 바로바로 정렬 가능
•
안정 정렬: 같은 값의 순서가 바뀌지 않습니다
•
작은 데이터에 효율적: 오버헤드가 적어서 n < 50 정도면 빠릅니다
•
구현 간단: 코드가 직관적입니다
•
역순 데이터에 최악: 매번 끝까지 밀어야 해서 O(n²)
•
무작위 데이터도 느림: 평균 O(n²)
언제 쓸까요?
- 데이터가 거의 정렬되어 있을 때
- 데이터가 실시간으로 들어올 때
- 작은 배열을 정렬할 때 (실제로 많은 고급 정렬 알고리즘들이 작은 부분에서는 삽입정렬을 씁니다!)
버블정렬 (Bubble Sort)
기본 개념
버블정렬은 인접한 두 원소를 비교하여 순서가 잘못되어 있으면 교환하는 방식입니다. 이 과정을 반복하면 가장 큰 값이 마치 거품(bubble)이 수면으로 떠오르듯이 배열의 끝으로 이동합니다.
코드는 단순하지만 효율이 낮아 실무에서는 거의 사용되지 않습니다. 주로 알고리즘 학습 목적으로 활용됩니다.
시간복잡도 분석
•
평균 (Average): O(n^2)
•
최악 (Worst): O(n^2) - 역순으로 정렬된 경우
•
최선 (Best): O(n) - 이미 정렬된 경우 (최적화 버전)
버블정렬 구현 코드 (개선된 버전)
void bubbleSort(std::vector<int>& arr)
{
int n = arr.size();
// 외부 루프: 배열 크기만큼 반복
for (int i = 0; i < n - 1; i++)
{
// 내부 루프: 아직 정렬되지 않은 부분만 비교
// 매 회전마다 가장 큰 원소가 뒤로 가므로 비교 범위가 줄어듭니다
for (int j = 0; j < n - 1 - i; j++)
{
// 인접한 두 원소 비교
if (arr[j] > arr[j + 1])
{
// 순서가 잘못되었으면 교환
std::swap(arr[j], arr[j + 1]);
}
}
}
}
C++
복사
코드 개선 사항:
1.
함수명 수정: bubleSort → bubbleSort (올바른 철자)
2.
효율성 개선: 내부 루프를 j < n - 1 - i로 설정
•
이유: 매 회전마다 가장 큰 원소가 배열 끝으로 이동하므로, 다음 회전에서는 그 부분을 다시 비교할 필요가 없습니다.
•
예: 1회전 후 마지막 원소는 확정, 2회전 후 마지막 2개 원소 확정...
최적화된 버블정렬 (조기 종료)
void bubbleSortOptimized(std::vector<int>& arr)
{
int n = arr.size();
for (int i = 0; i < n - 1; i++)
{
bool swapped = false; // 교환 발생 여부를 추적
for (int j = 0; j < n - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
std::swap(arr[j], arr[j + 1]);
swapped = true; // 교환이 발생했음을 표시
}
}
// 한 번의 전체 순회에서 교환이 없었다면 이미 정렬된 상태
if (!swapped)
{
break; // 조기 종료
}
}
}
C++
복사
최적화 원리:
한 번의 전체 순회(패스)에서 교환이 한 번도 발생하지 않았다면, 배열이 이미 정렬된 것입니다. 이 경우 더 이상 반복할 필요가 없으므로 루프를 종료합니다.
단계별 동작 과정
예시 배열: [5, 1, 4, 2, 8]
1회전: 8이 맨 뒤로!
2회전: 5가 뒤에서 두 번째로!
3회전: 정렬 완료!
삽입정렬 vs 버블정렬 비교
삽입정렬을 추천하는 경우:
•
작은 배열 처리 (n < 50)
•
거의 정렬된 데이터 (성능이 O(n)에 가까워짐)
•
온라인 정렬이 필요한 경우 (데이터가 하나씩 들어올 때)
•
안정 정렬이 필요한 경우
버블정렬을 사용하는 경우:
•
알고리즘 학습 목적
•
정렬 개념 이해를 위한 교육용
•
실제 프로젝트에서는 사용하지 않는 것을 권장합니다
병합 정렬 (Merge Sort)
한 줄 요약
"쪼개고 쪼개서 1개씩 만든 다음, 합치면서 정렬한다"
핵심 아이디어
병합정렬은 분할정복 전략을 사용합니다:
1.
분할: 배열을 반으로 계속 쪼갭니다 (원소 1개가 될 때까지)
2.
정복: 쪼개진 조각들을 정렬하면서 합칩니다
3.
결합: 정렬된 두 배열을 하나로 합칩니다
왜 1개까지 쪼갤까요? 원소 1개짜리 배열은 이미 정렬된 상태입니다!
시간복잡도 분석
•
최선 (Best): O(n log n)
•
최악 (Worst): O(n log n)
•
평균 (Average): O(n log n)
가장 큰 장점: 입력 데이터의 상태(정렬 여부, 중복 원소 등)와 관계없이 항상 안정적으로 O(n log n) 성능을 보장합니다.
시간복잡도 계산 과정 이해하기
병합정렬의 시간복잡도가 O(n log n)인 이유를 예를 들어 설명하겠습니다.
원소가 16개인 배열의 경우:
분할 단계 (트리의 깊이):
•
16개 → 8개씩 2개 (1단계)
•
8개 → 4개씩 4개 (2단계)
•
4개 → 2개씩 8개 (3단계)
•
2개 → 1개씩 16개 (4단계)
총 깊이: log₂(16) = 4단계
각 단계별 작업량:
•
4단계: 16개 노드 × 각 1개 비교 = 16번 작업
•
3단계: 8개 노드 × 각 2개 비교 = 16번 작업
•
2단계: 4개 노드 × 각 4개 비교 = 16번 작업
•
1단계: 2개 노드 × 각 8개 비교 = 16번 작업
총 작업량 계산:
일반적으로 n개 원소의 경우:
•
트리 깊이: log₂(n)
•
각 단계 작업: n번
•
총 작업: n × log₂(n)
병합정렬 완전 구현
#include <iostream>
#include <vector>
using namespace std;
int vect[5] = { 6, 1, 3, 8, 5 };
int result[5];
void run(int start, int end)
{
int mid = (start + end) / 2;
if (start >= end) return;
run(start, mid);
run(mid + 1, end);
// 두 영역 합치기 (result에 결과저장)
int a = start; // 영역은 start ~ mid 까지
int b = mid + 1; // 영역은 mid + 1 ~ end 까지
int t = 0;
while (1)
{
if (a > mid && b > end) break;
if (a > mid) //a 영역이 끝났으면 b영역값을 등록
result[t++] = vect[b++];
else if (b > end) //b 영역이 끝났으면 a 영역값을 등록
result[t++] = vect[a++];
else if (vect[a] <= vect[b]) // vect[a] 와 vect[b] 비교해서 작은것을 result에 넣기
result[t++] = vect[a++];
else
result[t++] = vect[b++];
}
// result에 있는 정렬된 배열을 vect에 적용
for (int i = 0; i < t; i++)
{
vect[start + i] = result[i];
}
}
int main()
{
run(0, 4);
// 정렬된 결과 출력
for (int num : vect)
{
cout << num << " ";
}
cout << endl;
return 0;
}
C++
복사
단계별 동작 과정
예시 배열: [6, 1, 3, 8, 5]
Step 1: 분할 단계 (쪼개기)
Step 2: 병합 단계 (합치면서 정렬)
최종 병합
병합하는 방법 (핵심!)
두 개의 정렬된 배열 \[6\]과 \[1, 3\]를 합칠 때:
포인터 → [6] [1, 3] ← 포인터
↑ ↑
1단계: 6 vs 1 → 1이 작음 → result = [1]
2단계: 6 vs 3 → 3이 작음 → result = [1, 3]
3단계: 6 vs 없음 → 6 추가 → result = [1, 3, 6]
JavaScript
복사
핵심: 두 배열의 맨 앞 원소만 비교하면 됩니다! 이미 정렬되어 있으니까요.
분할정복 전략의 3단계
1. 분할 (Divide):
•
배열을 절반으로 나눕니다.
•
재귀적으로 각 절반에 대해 같은 작업을 수행합니다.
2. 정복 (Conquer):
•
각 부분을 재귀적으로 정렬합니다.
•
기저 조건에 도달하면 (원소 1개) 정렬이 완료된 것으로 간주합니다.
3. 결합 (Combine):
•
정렬된 두 부분 배열을 하나의 정렬된 배열로 병합합니다.
장점과 단점
장점:
1.
안정적인 성능: 모든 경우에 O(n log n) 보장
2.
안정 정렬: 동일한 값들의 상대적 순서가 유지됩니다
3.
예측 가능: 최악의 경우에도 성능 저하가 없습니다
4.
대용량 데이터: 큰 데이터셋 처리에 매우 효율적입니다
5.
병렬 처리: 각 부분을 독립적으로 정렬할 수 있어 병렬 처리에 유리합니다
단점:
1.
추가 메모리: O(n)의 공간복잡도가 필요합니다 (임시 배열)
2.
재귀 오버헤드: 함수 호출 스택을 사용하므로 오버헤드가 있습니다
3.
작은 배열: 작은 데이터에서는 오버헤드로 인해 단순 정렬보다 느릴 수 있습니다
4.
캐시 효율: 메모리 접근 패턴이 불규칙하여 캐시 효율이 낮을 수 있습니다
최적화 기법
1. 작은 부분 배열에서는 삽입정렬 사용:
void mergeSort(int start, int end)
{
// 원소가 10개 이하면 삽입정렬 사용
if (end - start < 10)
{
insertionSort(vect, start, end);
return;
}
// 나머지는 기존 병합정렬 로직...
}
C++
복사
작은 배열에서는 삽입정렬이 더 빠르므로 이를 활용합니다.
2. 이미 정렬된 경우 병합 생략:
// 왼쪽 부분의 마지막 원소가 오른쪽 부분의 첫 원소보다 작거나 같으면
// 이미 정렬되어 있으므로 병합 불필요
if (vect[mid] <= vect[mid + 1])
{
return;
}
C++
복사
실전 활용 가이드
병합정렬을 사용해야 하는 경우:
•
안정적인 성능이 절대적으로 중요한 경우
•
안정 정렬이 필요한 경우 (동일 값의 순서 보존)
•
대용량 데이터를 처리해야 하는 경우
•
최악의 경우에도 성능을 보장해야 하는 경우
•
메모리가 충분한 환경
병합정렬을 피해야 하는 경우:
•
메모리가 제한적인 임베디드 시스템
•
작은 배열을 자주 정렬하는 경우
•
제자리 정렬이 필수인 경우
힙정렬 (Heap Sort)
기본 개념
힙정렬은 힙(Heap) 자료구조를 사용하는 정렬 알고리즘입니다. 선택정렬의 개선된 버전으로 볼 수 있습니다.
선택정렬과의 차이점:
•
선택정렬: 최댓값을 찾기 위해 O(n) 시간 소요 (선형 탐색)
•
힙정렬: 최댓값을 찾기 위해 O(log n) 시간 소요 (힙 사용)
힙 자료구조를 이용하면 최댓값 또는 최솟값을 효율적으로 찾을 수 있으므로, 이를 반복적으로 추출하여 정렬합니다.
힙(Heap) 자료구조란?
정의: 완전 이진 트리의 일종으로, 부모 노드와 자식 노드 간에 특정한 순서 관계를 유지하는 자료구조입니다.
힙의 종류:
1.
최대 힙 (Max Heap):
•
부모 노드의 값이 자식 노드의 값보다 크거나 같습니다.
•
루트 노드에 최댓값이 위치합니다.
2.
최소 힙 (Min Heap):
•
부모 노드의 값이 자식 노드의 값보다 작거나 같습니다.
•
루트 노드에 최솟값이 위치합니다.
힙의 주요 특징:
•
완전 이진 트리: 마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있고, 마지막 레벨은 왼쪽부터 채워집니다.
•
우선순위 큐 구현: 우선순위 큐를 구현하는 가장 효율적인 방법입니다.
•
빠른 접근: 루트 노드에 항상 최댓값(또는 최솟값)이 위치하므로 O(1)에 접근 가능합니다.
•
중복 허용: 이진 탐색 트리와 달리 중복된 값을 허용합니다.
시간복잡도 분석
•
평균 (Average): O(n log n)
•
최악 (Worst): O(n log n)
•
최선 (Best): O(n log n)
병합정렬과 마찬가지로 모든 경우에 안정적으로 O(n log n) 성능을 보장합니다.
시간복잡도 계산:
•
힙 구성: O(n)
•
n개의 원소를 하나씩 추출하면서 힙 재구성: n × O(log n) = O(n log n)
•
총 시간복잡도: O(n) + O(n log n) = O(n log n)
힙정렬 구현 (STL 사용)
#include <vector>
#include <queue>
#include <iostream>
void heapSort(std::vector<int>& arr)
{
// 1단계: 모든 원소를 우선순위 큐(최대 힙)에 삽입
// std::priority_queue는 기본적으로 최대 힙으로 동작합니다
std::priority_queue<int> maxHeap;
for (int i = 0; i < arr.size(); i++)
{
maxHeap.push(arr[i]); // 힙에 원소 삽입 - 각 삽입은 O(log n)
}
// 2단계: 힙에서 최댓값을 하나씩 꺼내어 배열에 저장
// 최댓값부터 꺼내므로 내림차순으로 정렬됩니다
for (int i = 0; i < arr.size(); i++)
{
arr[i] = maxHeap.top(); // 힙의 루트 (최댓값) 가져오기
maxHeap.pop(); // 힙에서 루트 제거 - O(log n)
}
}
int main()
{
std::vector<int> arr = {5, 2, 9, 1, 5, 6};
heapSort(arr);
// 정렬된 결과 출력 (내림차순)
for (int num : arr)
{
std::cout << num << " "; // 출력: 9 6 5 5 2 1
}
std::cout << std::endl;
return 0;
}
C++
복사
오름차순으로 정렬하려면:
// 최소 힙 사용
std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;
C++
복사
또는 최댓값부터 꺼내서 배열의 뒤에서부터 채웁니다:
for (int i = arr.size() - 1; i >= 0; i--)
{
arr[i] = maxHeap.top();
maxHeap.pop();
}
C++
복사
동작 과정 상세 설명
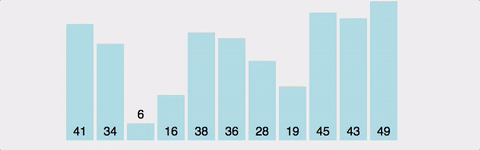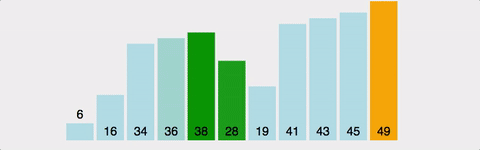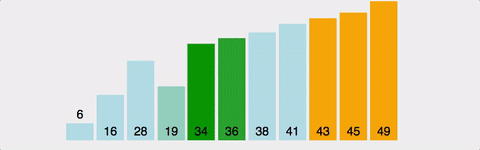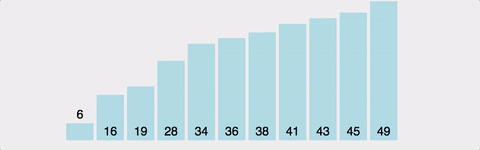
예시 배열: [5, 3, 1, 8, 7, 2, 4]
1단계: 힙 구성 (Heapify)
원소를 하나씩 최대 힙에 삽입하면서 힙 속성을 유지합니다:
2단계: 정렬 (Extract)
힙에서 최댓값을 하나씩 꺼냅니다:
선택정렬과 힙정렬 비교
비교 항목 | 선택정렬 | 힙정렬 |
최댓값 찾기 | O(n) - 선형 탐색 | O(1) - 힙의 루트 |
시간복잡도 | O(n²) | O(n log n) |
자료구조 | 배열만 사용 | 힙(트리) 구조 |
안정성 | 불안정 정렬 | 불안정 정렬 |
공간복잡도 | O(1) | O(n) - STL 사용 시
O(1) - 배열 기반 구현 시 |
배열 기반 힙정렬 구현 (제자리 정렬)
STL을 사용하지 않고 배열을 직접 힙으로 만드는 방법입니다. 이 방법은 추가 메모리가 필요 없습니다.
// 특정 노드를 루트로 하는 서브트리를 힙으로 만드는 함수
void heapify(std::vector<int>& arr, int n, int rootIdx)
{
int largest = rootIdx; // 루트를 가장 큰 값으로 초기화
int leftChild = 2 * rootIdx + 1; // 왼쪽 자식 인덱스
int rightChild = 2 * rootIdx + 2; // 오른쪽 자식 인덱스
// 왼쪽 자식이 존재하고 루트보다 크면
if (leftChild < n && arr[leftChild] > arr[largest])
{
largest = leftChild;
}
// 오른쪽 자식이 존재하고 현재 가장 큰 값보다 크면
if (rightChild < n && arr[rightChild] > arr[largest])
{
largest = rightChild;
}
// 가장 큰 값이 루트가 아니면 교환하고 재귀적으로 힙 속성 유지
if (largest != rootIdx)
{
std::swap(arr[rootIdx], arr[largest]);
heapify(arr, n, largest); // 영향받은 서브트리 재귀 처리
}
}
void heapSort(std::vector<int>& arr)
{
int n = arr.size();
// 1단계: 최대 힙 구성 (Build Max Heap)
// 마지막 비단말 노드부터 역순으로 heapify 수행
for (int i = n / 2 - 1; i >= 0; i--)
{
heapify(arr, n, i);
}
// 2단계: 힙에서 원소를 하나씩 추출하여 정렬
for (int i = n - 1; i > 0; i--)
{
// 현재 힙의 루트(최댓값)를 배열 끝으로 이동
std::swap(arr[0], arr[i]);
// 힙 크기를 1 줄이고 루트에 대해 heapify 수행
heapify(arr, i, 0);
}
}
C++
복사
코드 상세 설명:
heapify 함수:
•
특정 노드를 루트로 하는 서브트리가 힙 속성을 만족하도록 재구성합니다.
•
부모, 왼쪽 자식, 오른쪽 자식 중 가장 큰 값을 찾아 부모 위치로 이동시킵니다.
•
재귀적으로 아래쪽 서브트리도 처리합니다.
heapSort 함수:
•
첫 번째 for문: 배열을 최대 힙으로 변환합니다.
◦
n/2 - 1부터 시작하는 이유: 마지막 비단말 노드부터 처리하면 효율적입니다.
•
두 번째 for문: 힙에서 최댓값을 반복적으로 추출하여 배열 뒤쪽부터 채웁니다.
배열 인덱스 규칙 (0-based):
•
부모 노드: (i - 1) / 2
•
왼쪽 자식: 2 * i + 1
•
오른쪽 자식: 2 * i + 2
main 함수 사용 예시
int main()
{
std::vector<int> arr = {5, 3, 1, 8, 7, 2, 4};
std::cout << "정렬 전: ";
for (int num : arr)
{
std::cout << num << " ";
}
std::cout << std::endl;
heapSort(arr);
std::cout << "정렬 후: ";
for (int num : arr)
{
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
C++
복사
출력 결과:
장점과 단점
장점:
1.
안정적인 성능: 항상 O(n log n) 보장
2.
제자리 정렬: 배열 기반 구현 시 추가 메모리가 필요 없습니다 (공간복잡도 O(1))
3.
최악의 경우에도 효율적: 퀵정렬의 O(n²)보다 안정적입니다
4.
대용량 데이터: 큰 데이터셋 처리에 적합합니다
5.
우선순위 큐 응용: 힙 자료구조는 다양한 알고리즘에 활용됩니다
단점:
1.
불안정 정렬: 동일한 값의 상대적 순서가 변경될 수 있습니다
2.
캐시 효율: 배열 접근 패턴이 불규칙하여 캐시 미스가 많이 발생합니다
3.
구현 복잡도: 단순 정렬 알고리즘보다 이해하고 구현하기 복잡합니다
4.
평균 성능: 실제 속도는 퀵정렬보다 느릴 수 있습니다 (같은 O(n log n)이지만 상수 계수 차이)
실전 활용 가이드
힙정렬을 사용해야 하는 경우:
•
안정적인 성능이 절대적으로 중요한 경우
•
메모리가 제한적인 환경 (제자리 정렬 필요)
•
최악의 경우를 대비해야 하는 시스템
•
우선순위 큐 기반 알고리즘을 구현하는 경우
•
실시간 시스템에서 예측 가능한 성능이 필요한 경우
힙정렬을 피해야 하는 경우:
•
안정 정렬이 반드시 필요한 경우
•
캐시 효율이 중요한 경우
•
이미 부분적으로 정렬된 데이터 (삽입정렬이 더 효율적)