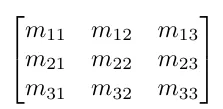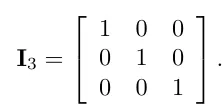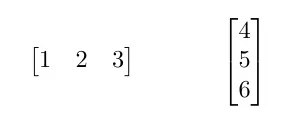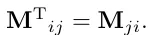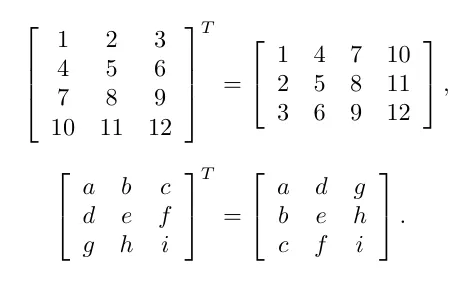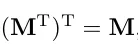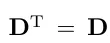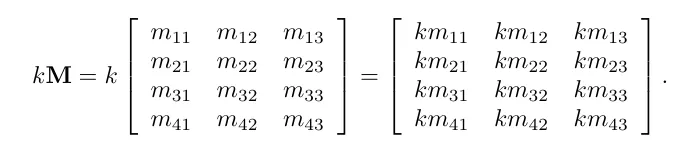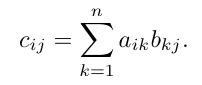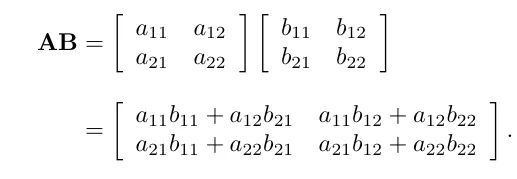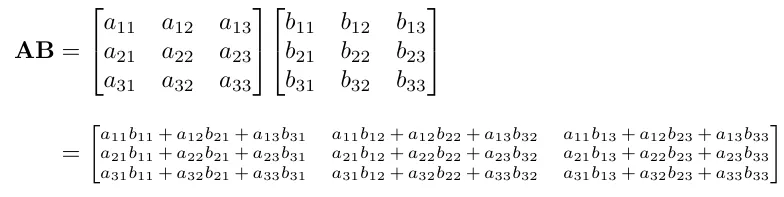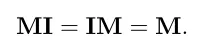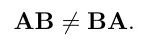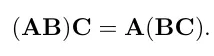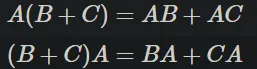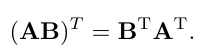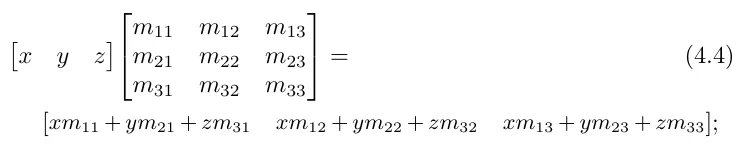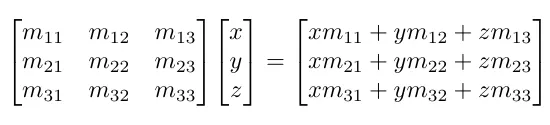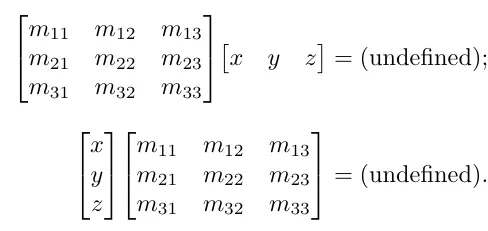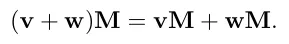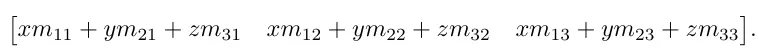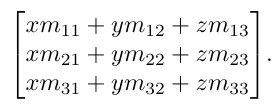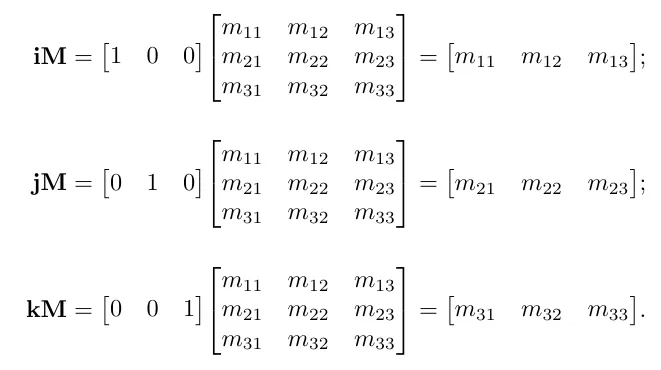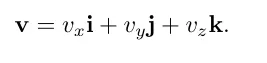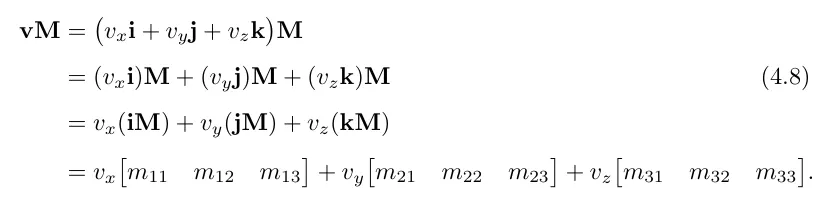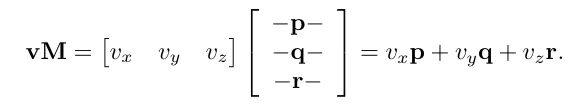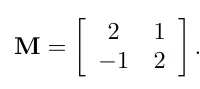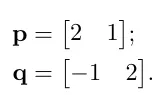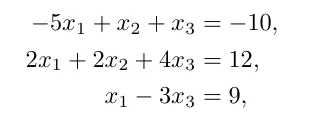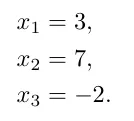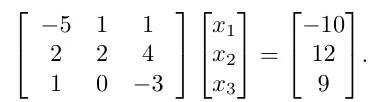행렬은 3D에서 매우 중요한 수학적 개념입니다. 다양한 좌표계 사이에서 중요한 역할을 합니다. 벡터를 이용한 좌표계를 표현할 때 서로 다른 좌표계간 변환 연산을 담당해줍니다.
이번 장에서는 행렬에 대해서 설명하겠습니다.
•
행렬의 기본 연산과 속성
•
기하학점 관점에서의 행렬의 속성
•
선형대수학에서의 행렬의 역할
등 3가지 경우로 설명하도록 하겠습니다.
행렬의 정의(mathematical definition of matrix)
선형대수학에서는 행과 열로 이루어진 사각형의 배열(2차원 배열)이라고 정의합니다.
벡터는 여러개의 스칼라로 이루어진 숫자의 집합이고 행렬은 여러개의 벡터로 이루어진 집합입니다.
행렬의 차수(Matrix dimensions and notation)
행렬은 행(row)와 열(column)으로 이루어져 있습니다. 몇개의 행과 열로 이루어져 있냐에 따라서 모양이 달라집니다. 예를들어 3X3행령은 4개의 행과 3개의 열을 가지고 있습니다.
정방행렬(square matrix)
행과 열이 같은 차수로 이루어진 행렬을 정방행렬이라고 합니다.
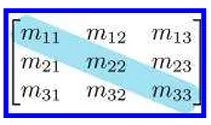
이중에서 각각의 행과 열이 마주치는 부분에만 값이 존재하는 행렬을 대각행렬(diagonal matrix)라고 합니다.
대각행렬중에서 각 값들이 전부 1로 이루어진 행렬을 단위행렬(identify matrix)라고 합니다.
단위 행렬은 종종 특정 상황에서 사용되기도 합니다. 앞으로 대문자 I 는 단위행렬이라고 기억해두시면 됩니다.
단위 행렬은 곱셈에 대한 항등식 연산이 성립하기 때문에 매우 특별합ㄴ디ㅏ.
특정행렬에 단위행렬을 곱하게 되면 해당 특정행렬의 값이 그대로 나오게 됩니다.
이 부분은 다음에 자세하게 설명 하도록 하겠습니다.
벡터와 행렬(vector as matrix)
벡터를 표현 할때 2가지 방법이 있습니다. 행벡터와 열벡터 입니다.
이 둘의 차이는 별로 중요하지 않지만 종종 이를 인지하고 사용해야할 때가 있습니다.
전치행렬( MatrixTransposition)
r x c 매트릭스M 가 있다고 생각해봅시다. 전치(transpose)는 로 표현합니다.
전치행렬은 r x c 를 c x r로 바꾸어서 표현 하는 행렬입니다. 즉 행렬의 요소 관계는
다음과 같습니다.
다른 예시로 벡터를 전치하면 다음과 같습니다.
전치 행렬을 다시 전치행렬 시키면 원본 행렬이 됩니다.
대각행렬의 전체행렬은 원본행렬과 같습니다.
행렬의 스칼라배 곱셈(Multiplying a matrix with a scalar)
행렬 M 에 스칼라k를 곱할수 있습니다. 행렬의 각 요소에 k를 곱해주면 됩니다.
두 행렬의 곱셈(Multiplying two matrices)
이번에는 두행렬을 곱해보도록 하겠습니다.
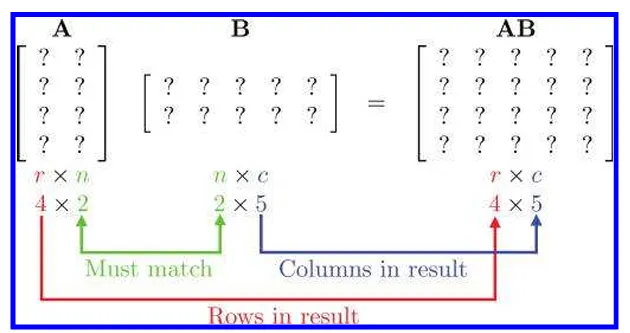
r x n 행렬 A와 n x c 행렬 B를 곱하면 r x c 매트릭스 AB가 나옵니다.
A행렬의 columns(열)과 B행렬의 row(행)이 일치하지 않으면 기본적으로 행렬의 곲셈 AB는 성립하지 않습니다.
행렬의 곱셈연산은 다음과 같습니다. 행렬 A(n x c) 와 행렬 B( n x c) 를 곱하여 행렬C(r x c)를 보면 행렬간의 곱셈은 내적과 관련이 있습니다. 행렬 곱셈에서 각 요소는 첫 번째 행렬의 행 벡터와 두번째 행렬의 열 벡터간의 내적을 통해 계산됩니다. C의 ij는 A의 i번째 행과 B의 j 번째 열간의 내적입니다.
이는 복잡해보이지만 사실 그림으로 펼쳐보면 매우 간단합니다.
2x2 행렬을 공식화 시켜보겠습니다.
3x3 을 공식화 시켜보겠습니다.
3D 그래픽스에서는 대부분 4x4행렬의 곱셈을 사용하게 됩니다. 이제 행렬의 곱셈과 덧셈 등등을 파악했으니 행렬의 곱셈에 대한 여러가지 특징에 대해서 알아보겠습니다.
•
단위행렬에 기존 행려을 곱하면 해당 행렬이 나옵니다.
•
교환법칙이 성립하지 않습니다.
•
결합법칙도 성립합니다.
•
분배법칙도 성립합니다.
•
행렬곱의 역행렬은 각각의 행렬의 위치를 바꾸어서 역행렬한 값과 같습니다.
행렬과 벡터의 곱셈
3D 그래픽스에서는 행렬간 곱셉만큼 벡터와 행렬간의 곱셈도 자주 사용됩니다.
3차원 벡터와 3x3행렬을 예시로 보겠습니다.
밑에 2가지 같은 경우는 행렬의 곱셈을 하기위 한 조건이 충족되지 않아 진행이 불가능합니다.
벡터와 행렬곱에 대한 몇가지 특징을 보겠습니다.
첫번째로 결과로 나오는 벡터의 각 요소는 행렬의 단일 행 또는 열이 있는 원래 벡터의 내적입니다.
두번째로 행렬의 각 요소는 벡터의 각요소에 작용하는 가중치로 볼수도 있습니다.
세번쨰로 두벡터의 덧셈에 행렬곱은 분배법칙이 성립합니다.
마지막으로 제일 중요한 점은 벡터에 행렬을 곱한다는건 아핀변환이 아닌 선형변환이라는 점입니다.
선형변환이라는 점이 우리가 3D 공간에서 한 벡터,점을 공간변환을 하는데 있어서 매우 중요합니다.
행벡터와 열벡터(row versus column vectors)
이번에는 행벡터와 행벡터와 열벡터의 구분이 중요한 이유를 알아보겠습니다.
행벡터 X 행렬을 곱하면 우리는 행(row) 벡터를 얻습니다.
반대로 행렬 X 열벡터 를 곱하면 우리는 열벡터를 얻습니다.
대부분의 산업에서는 열벡터가 표준으로 사용됩니다. 다만 3D 게임 프로그래밍에서는 컴퓨터 코드상에서 데이터를 표한하는데 행벡터가 가독성이 더 좋습니다. 그래서 우리 게임프로그래밍에서는 행벡터 기준으로 행렬연산을 진행하는 경우가 많습니다.
예시로 DirectX 에서는 행벡터를 사용합니다. OpenGL 에서는 열벡터를 사용합니다.
기하학적 관점에서의 행렬(Geometric interpretation of Matrix)
보통 행렬은 선형 변환을 표현합니다. 선형 변환이란 평행선을 보존하고 원점이 변하지 않는 변환입니다. 길이, 각도, 면적 같은 경우는 선형변환에서 변경 될수 있는 값들입니다. 좌표공간을 늘릴수는 있지만 곡선형이나 뒤틀거나 하는 변환을 하지 않습니다.
우리는 행렬이 좌표 공간의 변환을 나타낸다고 말했습니다. 행렬을 시각화 했을때 우리는 새로운 좌표 공간으로 변환하는 것처럼 보입니다. 그럼 변환이라는건 무엇 일까요?
3차원 공간과 3 x 3 행렬간의 관계는 무엇을 나타낼까요?
벡터를 변환하는데 있어서 행렬을 어떻게 구성해볼수 있을까요?
위 질문에 답하기 전에 표준 기저벡터에 행렬 M을 곱하면 어떻게 계산되는지 알아봅시다.
여기서 각각의 기저벡터 값을 활용하여 X,Y,Z의 벡터를 구성하는 3개의 행 벡터 값을 각 기저벡터에 곱해줘서 만들어지는 벡터 v를 얻을 수있습니다.
이 벡터 V에 행렬을 곱해보겠습니다.
최종 공식에서 우리는 기존 행렬에 Vx, Vy, Vz값을 기존 행렬에 값에 곱해진 선형변환이란걸 확인할수 있습니다. 또한 여기서 Vx, Vy, Vz를 기저벡터로 바꾸어서 생각해볼 수 있습니다.
행렬의 각 행들의 값을 간소화 시키면 다음과 같이 볼수 있습니다.
행렬이 표준 기저벡터를 변환하는 방법을 이해하면서 공간 변환에 대해서 알수 있습니다.
3x3 행렬은 계산하는데 복잡하니 2x2행렬로 바꾸어서 행렬과 공간변환에 대한 관계를 알아보도록 하겠습니다.
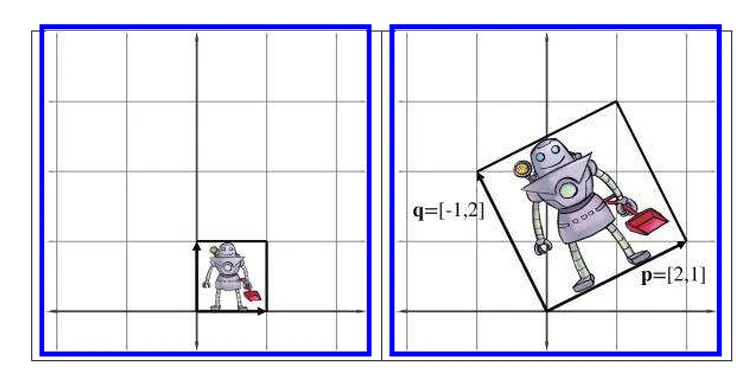
다음과 같은 행렬에서 각각의 행을 p, q로 뽑을수 있습니다.
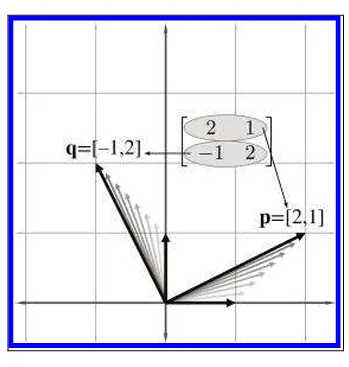
표준 기저벡터에서의 좌표계에서 해당 행렬을 곱하면 다음과 같은 그림으로 표현 할 수 있습니다.
x 기저벡터는 p 벡터로 변환되고 y 기저벡터는 q벡터로 변환됩니다. 얼추 각도로 보면 26.5도정도 회전하고 길이도 증가하였습니다.
기저벡터가 영향을 받는 다는건 모든 벡터들이 기저벡터가 변하는 만큼의 영향을 받는다고 할수 있습니다.
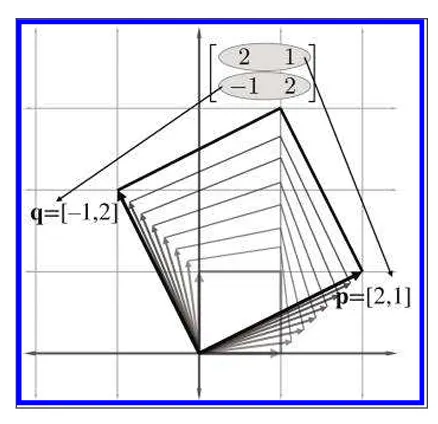
여기서 우리는 x,y 기저벡터로 이루어진 정사각형이 p,q로 이루어진 평행사변형을 완성함으로써 미치는 공간이 회전하고 늘어난걸 볼 수 있습니다.
이 평행사변형을 스큐박스라고 합니다.
여기서 행렬 M이 좌표공간을 회전시킬 뿐만 아니라 크기도 조정합니다.
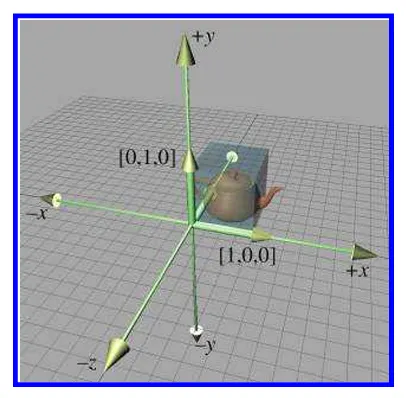
이제는 2D변형을 3D 로 시각화 시켜보겠습니다. 3D에서는 표준기저벡터 x,y,z,로 확장시키면 됩니다.
여기에 다음 3x3 행렬을 이용해서 변환시켜 보겠습니다.
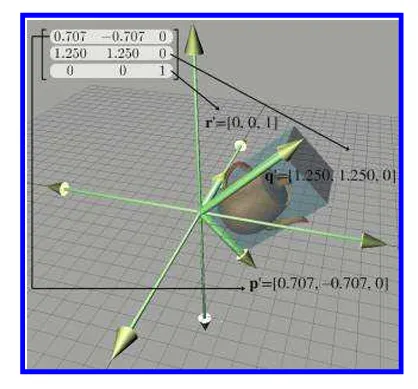
2D 때와 마찬가지로 기저벡터를 회전시키고 좌표계를 변환시켜표현하면 다음과 같이 주전자가 회전하고 바뀝니다.
주전자는 45도정도 회전하고 위로 길어졌습니다. 그리고 옆으로는 줄어들고 행렬에 3번째 벡터 z는 [0,0,1]이기 때문에 변환이 진행되지 않았습니다.
그럼 위내용 들을 정리해보겠습니다.
•
정사각 행렬은 좌표 공간에서 기저벡터로 해석 될수 있습니다.
•
새로운 좌표 공간으로 변환하려면 벡터에 행렬을 곱하면 됩니다.
•
행렬을 이용한 좌표공간의 변환은 선형변환입니다. 선형 변환은 직선을 유지하고, 평행성을 유지합니다. 그러나 각도, 길이, 면적, 볼륨은 행렬곱 이후에 변할 수 있습니다.
•
0벡터에 정사각행렬을 곱하면 결과는 0벡터가 나옵니다. 그말인 즉슨 어떤 좌표공간으로 변환하더라도 행렬곱으로 변환을 진행한다면 원점이 유지 된다는 점입니다.
•
우리는 행렬의 곱을 기저벡터의 좌표공간 변환으로 시각화 할 수 있습니다.
선형대수학에서의 큰 그림
선형 대수학은 벡터와 행렬의 기하학적 응용에 초점을 두고 있습니다.
이제 기본적인 관계를 설명 했으니 우리는 이들이 3D 그래픽스에서 어떤 영향과 역할을 하는지 알아볼것입니다.
이제는 우리가 원하는 방정식을 행렬식으로 바꾸어서 표현할수 있습니다.
위 방정식을 구하는데 있어서 방정식 풀이법을 이용해서 하나의 원소씩 계산하여 구할수 있지만 다음과 같이 행렬을 사용하면 더 빠르게 계산이 가능해집니다.
방정식을 사용해서 대부분의 게임프로그래밍을 로직을 작성 할수 있지만 하드웨어(GPU)의 발전으로 인해서 병렬연산을 이용하기 위해 선형대수학(행렬)을 이용하여 계산할 경우 더 많은 계산을 동시에 계산할수 있게 됬습니다.
또한 일반적인 캐릭터 작동 로직외에 화면에 물체를 그리는데 들어가는 기술적 로직들 유체, 천, 헤어, 머신비전, 모션 인식, 글로벌 일루미네이션 등등 에서 선형대수학의 힘은 더욱더 발휘할 것입니다.